TEKIS KESIMLARNING GEOMETRIK XARAKTERISTIKALARI Reja: 1. Umumiy tushunchalar. 2. Kesimning statik momenti 1

3.Tekis kesimlarning geometrik xarakteristikalari. Bizga ma’lumki sterjen cho’ziishi yoki siqilishida uning ko’ndalang kesimida kuchlanish hosil bo’ladi. Bu esa deformatsiya potensial energiyasini keltirib chiqaradi, ya’ni potential energiya sterjen ko’ndalang kesimiga bog’liq bo’ladi. Yuza kundalang kesim xarakteristikalaridan bog’liq. Agar ko’ndalang kesimni bir qancha elementar dF yuzachalardan iborat deb qarasak ushbu kesim yuzasi F=∫ dF (1) bo’ladi. Egilish, buralish yoki murakkab qarshiliklarni hisoblashda hisob ishlarida kesim geometric xarakteristikalarining murakkabligi muhim rol uynaydi. Bular quyidagilar, statik moment kesim qutb inersiya momenti, kesim markaziy inersiya momentlari hisoblanadi. Bu hollarda (1) tenglama integrali ostidagi dF elementar yuzacha o’rniga koordinatalar y,z,ρ lar ishtirok etadi. Bundan ko’rinadiki kesim geometrik xarakteristikasi nafaqat tuzilishidan balkim o’qlarning joylashishidan ham bog’liq bo’ladi (1-ram). (1-ram) 2. Kesimning statik momenti. 2

Kesimning statik momenti deb bir nechta elementar yuzachalar dF larning umumiy yig’indisi F bilan ular joylashgan o’qqacha bo’lgan masofasi ko’paytmasiga aytiladi. Sz=∫ F ydF , Sy=∫ F zdF (2) Statik moment birligi sm 3;m3 larda ifodalanadi. Murakkab kesimlarnig bir o’qqa nisbatan statik momenti deb shu o’qqa nisbatan barcha qismlari static momentlarining yig’indisiga aytiladi. Bir-biriga parallel joylashgan z va z1 o’qlarga nisbatan statik momentlar bog’liqligini qarab chiqamiz (2-rasm) 2-rasm (2) formulaga binoan o’qlarga nisbatan statik moment quyidagicha bo’ladi. σ ок = А ок A 0 Bu yerda y1= y−a bo’lgani uchun σ bx = F b A 0 (3) Xuddi shunday Sy1=∫ F (y−b)dF =∫ F ydF −b∫ F dF =Sy−bF ; (4) Endi z1 va y1 o’qlarning joylashishini aniqlaymiz (3-rasm). Buning uchun (3) va (4) ifodalar statik momentlarini nolga tenglaymiz. Sz1= Sz− ycF= 0; Sy1= Sy− zcF= 0 bundan 3

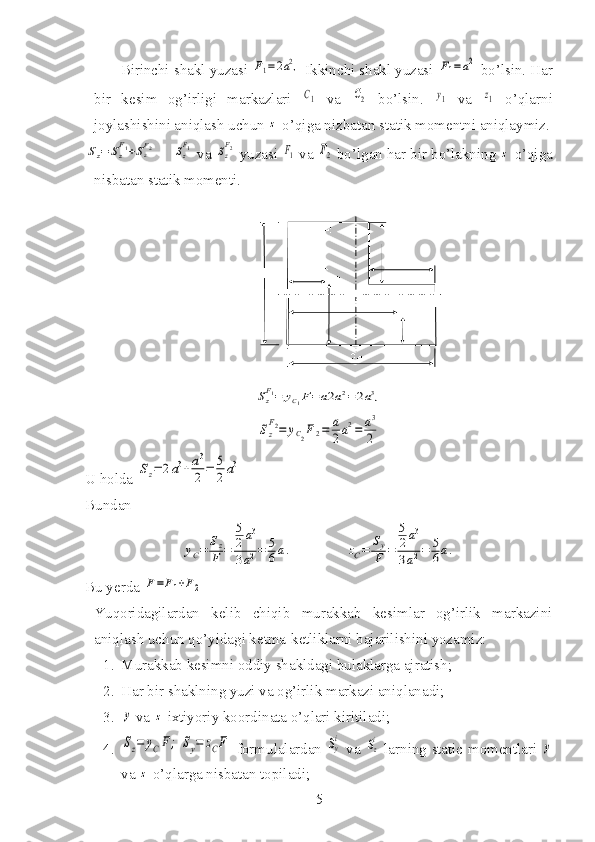
yc= Sz F ; zc= Sy F . (5) y va z o’qlarining kesishish nuqtasiga nisbatan С nuqtaganing og’irlik markazi deyiladi. Og’irlik markazi orqali o’tgan o’qga markaziy o’q deyiladi. Kesim og’irlik markazi o’tgan ixtiyoriy o’qqa nisbatan statik momenti nolga teng. (5) formula kesim og’irlik markazi koordinatalarini aniqlashda qullaniladi. (3-rasm) Kesim og’irlik markazi aniq bo’lsa, kesim statik momentlari ixtiyoriy y va z o’qlariga nisbatan quyidagicha bo’ladi. (4-rasm). Sc= ycF; Sc=zcF. (6) (4-rasm) Og’irlik markazlari 5-rasmda tasvirlangan masalani qarab chiqamiz. Buning uchun shaklni bulaklarga ajratamiz. 4

Birinchi shakl yuzasi F1=2a2, Ikkinchi shakl yuzasi F1=a2 bo’lsin. Har bir kesim og’irligi markazlari C1 va C2 bo’lsin. y1 va z1 o’qlarni joylashishini aniqlash uchun z o’qiga nizbatan statik momentni aniqlaymiz. Sz= Sz F1+SzF2 Sz F1 va Sz F2 yuzasi F1 va F2 bo’lgan har bir bo’lakning z o’qiga nisbatan statik momenti. Sz F1= yC1F=a2a2=2a3, Sz F2= yC2F2= a 2a2= a3 2 U holda Sz= 2a3+a3 2 = 5 2a3 Bundan yC= Sz F = 5 2a3 3a2= 5 6a. zC= Sy F = 5 2a3 3a2= 5 6a. Bu yerda F=F1+F2 Yuqoridagilardan kelib chiqib murakkab kesimlar og’irlik markazini aniqlash uchun qo’yidagi ketma-ketliklarni bajarilishini yozamiz: 1. Murakkab kesimni oddiy shakldagi bulaklarga ajratish; 2. Har bir shaklning yuzi va og’irlik markazi aniqlanadi; 3. y va z ixtiyoriy koordinata o’qlari kiritiladi; 4. Sz= yCF; Sy= zCF formulalardan Sy i va Szi larning static momentlari y va z o’qlarga nisbatan topiladi; 5