Berilgan burchakka teng burchakni yasash
















Mavzu: Berilgan burchakka teng burchakni yasash
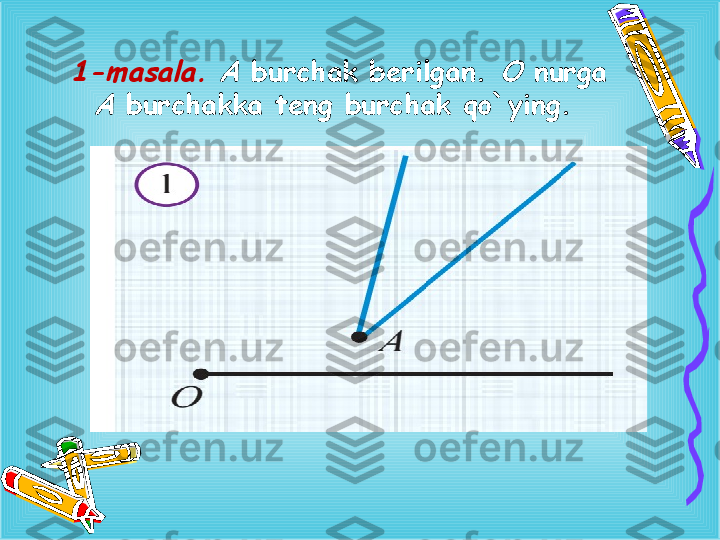
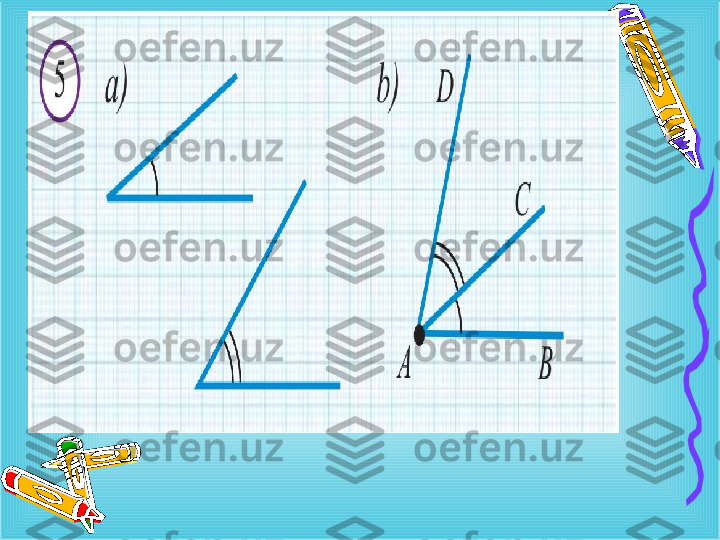
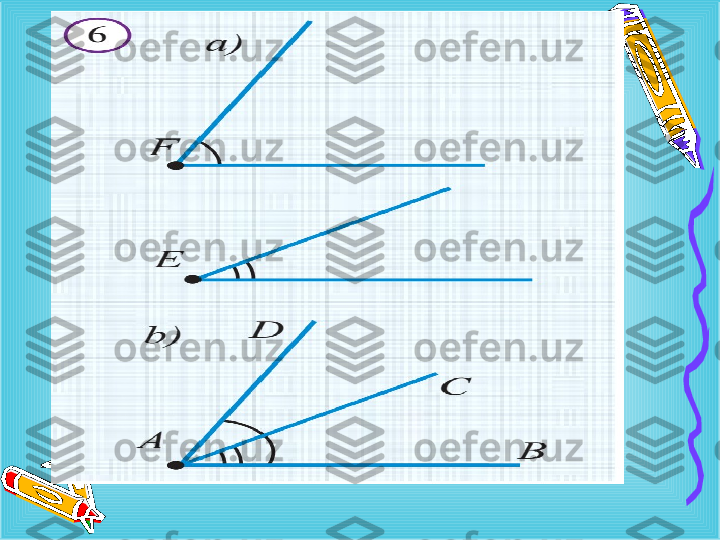
1-masala. A burchak berilgan. O nurga A burchakka teng burchak qo ` ying.
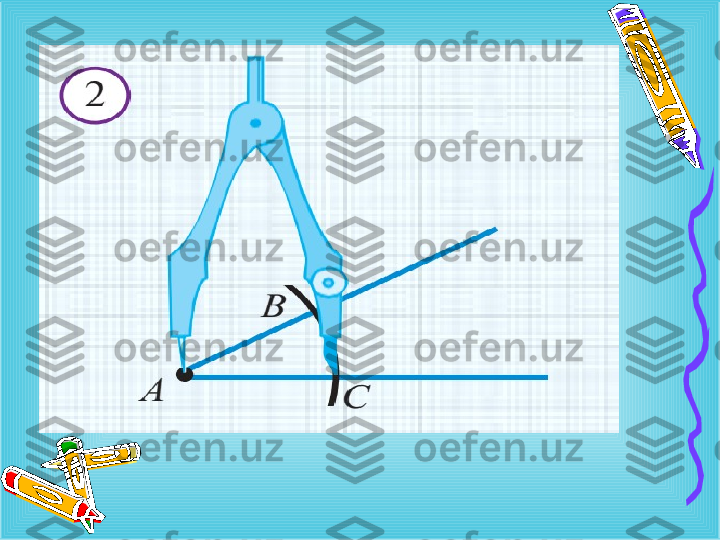
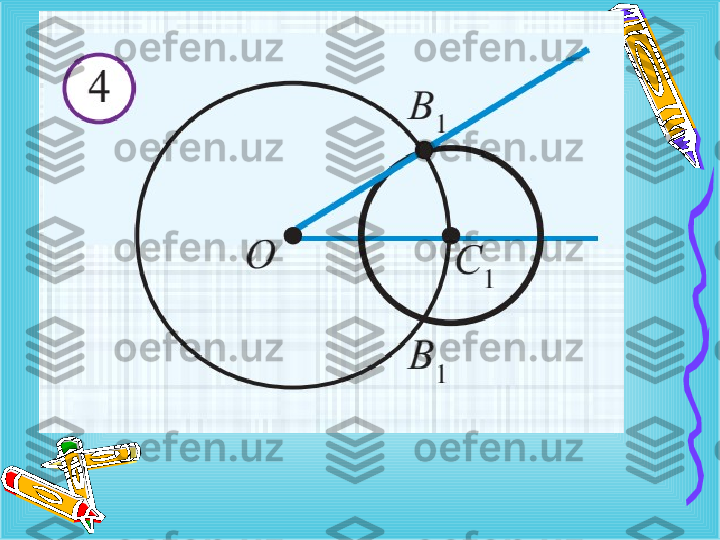
Yasash: 1-qadam . Markazi A nuqtada bo ` lgan ixtiyoriy aylana chizamiz . Bu aylana berilgan A burchak tomonlarini B va C nuqtalarda kesib o ` tsin.
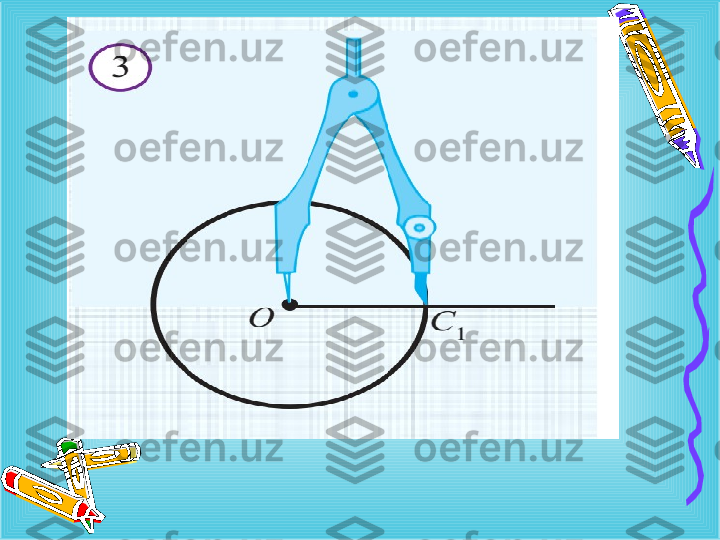
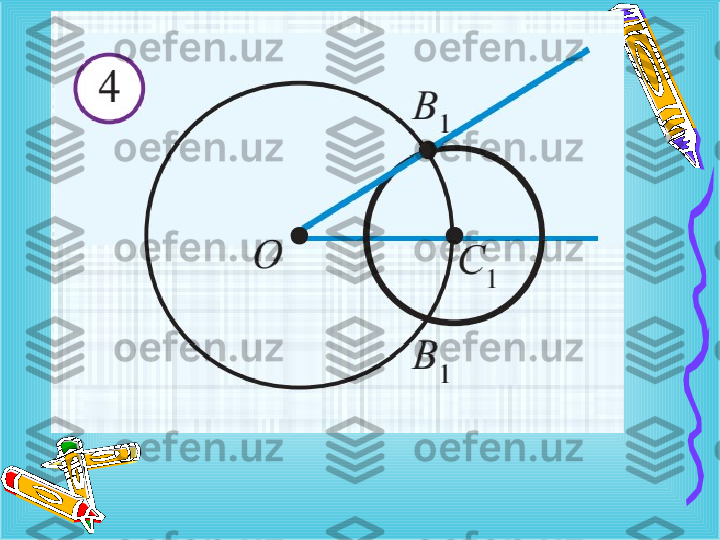
2-qadam . Radiusi chizilgan aylana radiusiga teng va markazi O nuqtada bo ` lgan aylana chizami z . Bu aylananing O nur bilan kesishish nuqtasini C bilan belgilaymiz. ₁
