logo
  1. Bosh sahifa
  2. Slaydlar
  3. Umumiy
  4. Sonning butun qismi

Sonning butun qismi

Yuklangan vaqt:

10.08.2023

Ko'chirishlar soni:

0

Hajmi:

1168.6162109375 KB
Ko'chirib olish
i9 presentation to Joe Smith1 Mavzu: Sonning butun qismi i9 presentation to Joe Smith2 Maqsad : Sonning butun qismi funksiyasi bilan tanishish Sonning butun qismi funksiyasi grafigini yasash Mustaqil misollar yecha olish ko` nik masini shakllantirishButun qism funksiyasi qo` llanilishiga doir misollar yechish . 1 2 3 4 i9 presentation to Joe Smith3Sonning butun qismi Sonning butun qismi deb, shu sondan katta bo`lmagan butun sonlar ichida eng kattasiga aytiladi va [x] kabi belgilanadi. Masalan, [3,45]=3, [-2,5]=-3, [2]=2 , [0.23]=0 i9 presentation to Joe Smith4Sonning butun qismi Sonning butun qismi funksiyasi “ant`ye” funksiyasi deb ham ataladi. i9 presentation to Joe Smith5 y=[x] funksiya grafigi ZyZxE RxRyD   ,)( ,)( i9 presentation to Joe Smith6Ant`ye funksiyasi xossalari: .,,y-x holda u bo`lsa, [y][x] Agar 6. Z; R,xagar m,x][][x. [0;1); Z,xagar x,]4.[x R;xagar 1,x][x[x] 3. R;xagar x,[x]1-x 2. Z;xagar x,[x] 1. Ryxmm       15  i9 presentation to Joe Smith7 1 n sonidan k at t a bo` l maga n nat ural sonl ar i chida necht asi k soniga qoldiqsiz bo` linadi?     k n • 100 dan katta bo`lmagan natural sonlar ichida nechtasi 7 ga qoldiqsiz bo`linadi? 14 7100      i9 presentation to Joe Smith8 1 [n;m ] k esmada joy l ashgan sonlardan necht asi k soniga qol diqsiz bo` linadi? 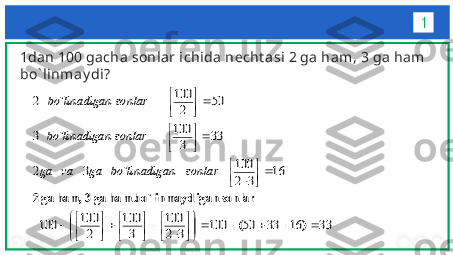Nnm ,           kn km 1 • Barcha uch xonali natural sonlar ichida nechtasi 7 ga qoldiqsiz bo`linadi?128 14 142 7 99 7 999             i9 presentation to Joe Smith9 1 • 1 dan N gacha natural sonlar ichida nechtasi a ga ham, b ga ham bo`linmaydi ?                      b a N b N a N N i9 presentation to Joe Smith10 1 1 da n 100 gacha sonl ar i chida necht asi 2 ga ham, 3 ga ham bo` li nmay di?33 16 33 50 100 3 2 100 3 100 2 100 100 16 3 2 100 3 2 33 3 100 3 50 2 100 2                                     ) ( sonlar igan bo`linmayd ham ga 3 ham, ga 2 ` ` ` sonlar linadigan bo ga va ga sonlar linadigan bo sonlar linadigan bo i9 presentation to Joe Smith11 1 • 1 dan N gacha natural sonlar ichida nechtasi a ga ham, b ga ham, c ga ham bo`linmaydi ?                                        c b a N c a N c b N b a N c N b N a N N i9 presentation to Joe Smith12 1 • 1 dan 100 gacha natural sonlar ichida nechtasi 2 ga ham, 3 ga ham, 5 ga ham bo`linmaydi ? 26310616203350100 532 100 52100 53100 32100 5100 3100 2100 100                                          )( i9 presentation to Joe Smith13 • 21! ni tub ko`paytuvchilarga ajrating. 8765 43 21 1917131175322120432121         ...! 18 1 2 5 10 2 21 2 21 2 21 2 21 2 21 5 4 3 2 1                                ...  927 3 21 3 21 321 322                  1 19 21 1 17 21 1 13 21 1 11 21 3 721 4 521 87 65 43                                        111134918 19171311753221 ! i9 presentation to Joe Smith14 DTM 2019 toping. qiymatini ning n bo`lsa, son toq ifoda 411! son. butunmusbat - n n nn CC 28 2 22 22 1    n 411!Suratdagi ifodada 2 ning darajasini aniqlaymiz 8 1 2 5 2 11 2 11 2 11 3 2 1               2n=8 n=4 i9 presentation to Joe Smith15 DTM 2019 toping. qiymatini kichik eng ning b bo`lsa, ! ! A 7aA Agar sonlardir. natural b va a b      42150 a B C A     18 624 7 77 42150 ! ! b=18 6 742 24321 7150 7150 2                i9 presentation to Joe Smith16 toping qiymatini katta eng ning n bo`ladigan son natural ifoda ! n 640  n n n n C C 3 2 3 2 3 2 6 40 18 38 18 38         3 2 ! n=18   yetarli ko`rish darajasini gkattasinin sonlaridan b va a uchun bo`linishi qoldiqsiz ga ba ifoda.... n  3 21 532    i9 presentation to Joe Smith17 DTM 2019 nnn 52 52 52 52 0   ! )( ! 1 52! n n=12 Berilgan son 12 ta nol bilan tugaydi.52! ifoda nechta nol bilan tugaydi? Bu sonni 10 ning qanday eng katta darajasiga bo`linishini topishimiz yetarli12 2 10 5 52 5 52 2             i9 presentation to Joe Smith18 DTM 2019 toping. qiymatini kichik eng ning b bo`lsa, 60! sonlardir. natural b va a b a 21  bbb 7321  C 928 7360 ! Ca bb  928 7373 b=9 i9 presentation to Joe Smith19 • Tenglama yechimga ega bo`lishi uchun n soni albatta butun bo`lishi kerak! Aks holda tenglama yechimga ega bo`lmaydi yechiladi keltirilib katengsizlik 1nxn tenglamani n[x] ko`ra xossasiga funksiyasi qismi butun Sonning  yeching tenglamani n[x]  i9 presentation to Joe Smith20 • Javob: (-4;-1,5] ],;( );( );(],;(1-x 5x yeching Tenglamani 514 14 151 0 1 4 0 1 32 4 15 3 15 43 3 15                              xx x x x xx x x x i9 presentation to Joe Smith21 5 4 15 7 5 4 1 5 715 15 7 0 5 715 31 30 1 30 131 40403910 403910 1 40 3910 40 3910 1 40 3910 40 3910 15 75 8 6 8 5 15 75 5 715 5 715 21                                                xxjavob xx xx t tt tt tt tt tt tt ttt tt t xtx x ,: ko`ramiz xollarni 1t va 0t nekanligida son butunt , ,8 6x5 son. butunt Bunda•kiritamiz. Belgilash• 8 6x5 yeching Tenglamani i9 presentation to Joe Smith22 1 2 142 14 2 14 4 12 4             tt t tt t xtx 12x [x]yeching tenglamani 1 2x- 4[x]  i9 presentation to Joe Smith23 chizamiz nigrafiklari funksiya yechamiz. usulda grafik va olamiz keltirib shaklga 12x [x] Tenglamani         4 12 4 x y xy yeching tenglamani 1 2x- 4[x]  Grafiklar bitta nuqtada kesishadi. x=1,5 i9 presentation to Joe Smith2462, 3 x 5x yeching Tenglamani      olmaydi bo`la teng ga 2,6 qismi butun sonning sababi emas, ega yechimga Tenglama i9 presentation to Joe Smith25 Test teng? nechaga yig`indi cba bo`lsa, o`rinli tenglik 5328!-6! uchunsonlar butunmusbat c va b a, 1. cb   a 2 a) 11 b) 12 c) 10 d) 9 i9 presentation to Joe Smith26 Test a) 81 b) 82 c) 80 d) 90• 2. Nechta uch xonali natural son 11 ga qoldiqsiz bo`linadi? i9 presentation to Joe Smith27 Test a) 10 b) 11 c) 8 d) 18• 3. 25! soni 3 ning qanday eng katta darajasiga qoldiqsiz bo`linadi? i9 presentation to Joe Smith28 Test a) 10 b) 11 c) 14 d) 12• 4. 23∙24∙…∙60 soni 5 ning qanday eng katta darajasiga qoldiqsiz bo`linadi? i9 presentation to Joe Smith29 Test a) 131 b) 130 c) 150 d) 69• 5. 200 dan katta bo`lmagan natural sonlardan nechtasi 2 ga ham, 5 ga ham, 7 ga ham bo`linmaydi? i9 presentation to Joe Smith30 Test a) 1 b) 3 c) 4 d) 2• 6. [x]=3 bo`lsa, x nechta butun qiymat qabul qila oladi? i9 presentation to Joe Smith31 Test a) 4,6 b) 1,6 c) 2,6 d) 5,6• 7. Hisoblang [-3,25]+1,6+[7,25]= i9 presentation to Joe Smith32 Test a) -3 b) -4 c) -2 d) -5      359919908  )(,,. Hisoblang i9 presentation to Joe Smith33 Test a) 2 b) 3 c) 0 d) 1 59      4 13-3x bor ildizi butun nechta ngTenglamani. 337 11 37333 2413320 6     x x x 4 13-3x 5 i9 presentation to Joe Smith34 Test a) [-7,5;-5,5) b) [-7,5;-5,5] c) (-7,5;-5,5) d) (-7,5;0] 210       2 3,5x yeching Tenglamani. i9 presentation to Joe Smith35 Xulosa • Sonning butun qismi funksiyasi umumiy o`rta ta`lim maktablarida chuqur o`rganilmaydi. Faqatgina sonning butun qismini topish topishga doir ma`lumotlar keltirilgan. Lekin yuqorida ko`rib o`tilgan va shunga o`xshash misollar orqali o`quvchilarni yanada fanga qiziqtirish mumkin. • Bu tipdagi misollarni darsdan tashqari mashg`ulotlarda ko`rib chiqish tavsiya etiladi.

i9 presentation to Joe Smith1 Mavzu: Sonning butun qismi

i9 presentation to Joe Smith2 Maqsad : Sonning butun qismi funksiyasi bilan tanishish Sonning butun qismi funksiyasi grafigini yasash Mustaqil misollar yecha olish ko` nik masini shakllantirishButun qism funksiyasi qo` llanilishiga doir misollar yechish . 1 2 3 4

i9 presentation to Joe Smith3Sonning butun qismi Sonning butun qismi deb, shu sondan katta bo`lmagan butun sonlar ichida eng kattasiga aytiladi va [x] kabi belgilanadi. Masalan, [3,45]=3, [-2,5]=-3, [2]=2 , [0.23]=0

i9 presentation to Joe Smith4Sonning butun qismi Sonning butun qismi funksiyasi “ant`ye” funksiyasi deb ham ataladi.

i9 presentation to Joe Smith5 y=[x] funksiya grafigi ZyZxE RxRyD   ,)( ,)(

O'xshashlar

Sonning moduli
Sonning moduli .Modulli tengsizliklar
Qismga ko’ra sonning o’zini topish
Tuproqning organik qismi va unumdorligi
QARAMA-QARSHI SONLAR. SONNING MODULI