Tanlash usuli bilan kombinatorik masalalarni yechish

Kombinatorika « kombinatorika » atamasi lotincha combinare – « birlashma , tanlanma » degan so‘zdan kelib chiqqan . Ta’rif . Kombinatorika – bu matematikaning bir bo‘limi bo‘lib, turli to‘plam elementlarini tanlab olishlari yoki ularning joylashishlari sonini topish bilan shug‘ullanadi.

Qo‘shish qoidasi : Agar qandaydir A obyektni m ta usul bilan, boshqa B obyektni esa n xil usul bilan tanlab olish mumkin bo’lsa, “A yoki B” tanlovni m+n xil usul bilan tanlab olish mumkin. Misol : Likopchada 5 ta olma va 4 ta apelsin bor. Bitta mevani necha xil usulda tanlab olishimiz mumkin? Yechim : Masala shartiga ko‘ra olmani besh xil usul bilan, apelsinni esa to‘rt xil usul bilan tanlab olish mumkin. Masalada esa bitta mevani, ya’ni “ olma yoki apelsin” tanlovini qo‘shish qoidasi ga asosan 5+4=9 xil usul bilan amalga oshirish mumkin . Javob : 9 xil usul .

Masala : 1, 4, 7 raqamlaridan foydalanib, raqamlari takrorlanmagan nechta ikki xonali sonlar tuzish mumkin? Yechish : 1 usul: Variantlarni sanash . Sonlarni birortasini ham qoldirmaslik uchun, ularni o‘sish tartibida joylashtiramiz. Avval 1 raqami bilan, so‘ngra 4, va nihoyat 7 raqami bilan boshlanadigan sonlarni yozib chiqamiz : 14, 17, 41, 47, 71, 74. Javob : 6 ta son .

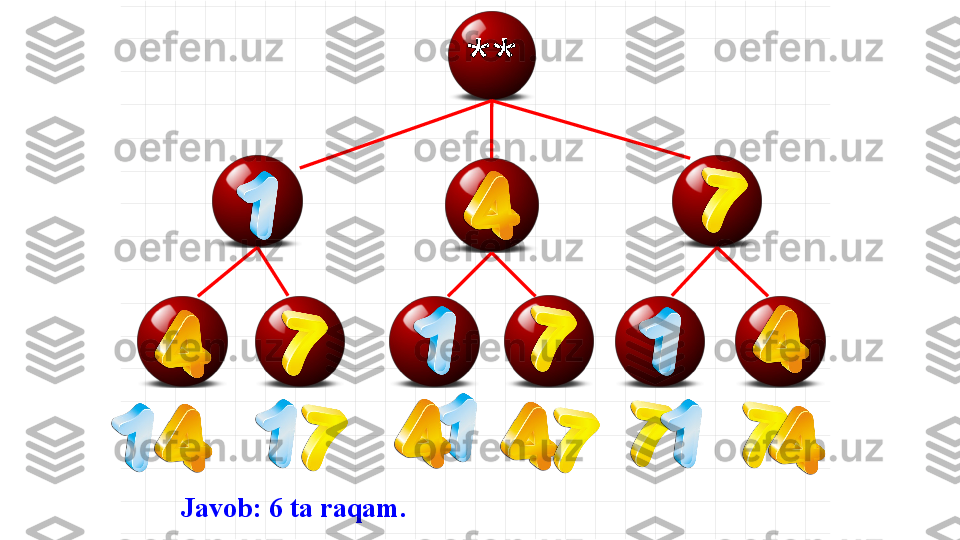
Masala : 2 usul : “Daraxtsimon” usul . Buning uchun, maxsus sxema tuzib olamiz: Yulduzcha chizib olamiz . So‘ngra bu yulduzchadan 3 ta kesma chiqaramiz. Masala shartida 3 ta raqamlar – 1, 4, 7 berilgani uchun bu kesmalarning ikkinchi uchiga shu raqamlarni yozamiz.Natijada 14, 17, 41, 47, 71,74 sonlari hosil bo’ldi. Bu sxema rostdan ham daraxtga o‘xshaydi, faqat “to‘nkarilgan” holatda bo’ladi.