Yuzalarni hisoblashda aniq integraldan foydalanish










Dars maqsadlari: O'quv maqsadi : egri chiziqli trapetsiya yuzi va integral haqida tushuncha berish Rivojlantiruvchi maqsad : sabab-oqibat munosabatlarini o'rnatish orqali maktab o'quvchilarining mantiqiy tafakkurini rivojlantirish. Motivatsion maqsad : mavzuni o'rganishga qiziqish uyg'otish
F(x) funksiyalarning qaysi biri f(x) funksiyaning boshlang’ich hosilasi hisoblanadi? ? ? ? ? ? ?( ) 2 3 f x x 2( ) 3F x x x 2 ( ) 3 2F x x x 2 ( )F x x 2 ( ) 5 3F x x x 2 ( ) 3 10F x x x 2 ( ) 3F x x
f(x)=sin x funksiya uchun boshlang’ich funksiya bo’ladimi ?( ) sin cos 3 F x x ? ( ) sin cos 4 F x x ? ( ) sin cos F x x x ( ) cos 12 F x x ( ) 8 cos F x x ? ( ) 1 cos F x x ( ) 1 cos F x x ( ) cos F x x ?
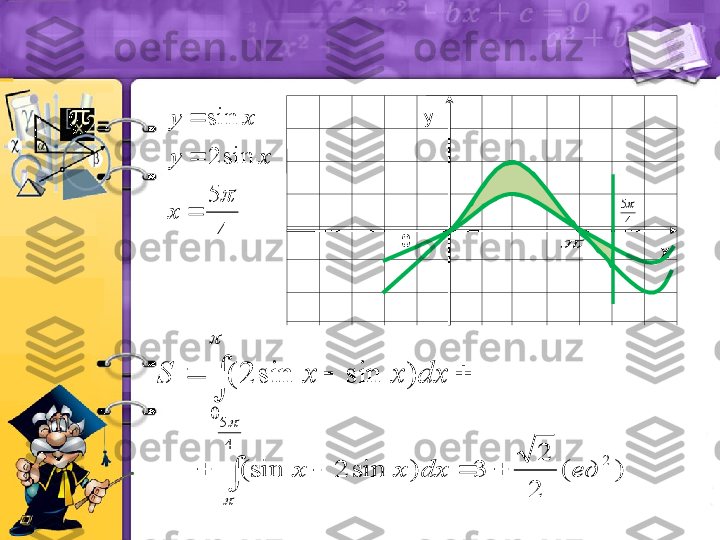
Integral asoschilari) ( ) ( ) ( a F b F dx x f b a b a dx x f S ) ( Isak Nuyuton 1643-1727 Gotfrid Leybnis 1646-1716
