Chiziqli differensial tenglamalar sistemasini matritsaviy usulda yechish













![H =(
V11 V12
V21 V22)=(
−1 1
1 0).
H−1 teskari matritsasi esa quyidagicha:
H − 1
= 1
∆
( A
11 A
12
A
21 A
22 ) T
= 1 (
− 1 )( 0 − 1
− 1 − 1 ) T
= − ( 0 − 1
− 1 − 1 ) = ( 0 1
1 1 ) .
Bunda, A
ij − H
matritsaning algebraik to’ldiruvchisi,
∆− ¿ det(H).
Oxirgi almashtirishlardan so’ng, Jordan shakli ekanigiga ishonch hosil
qilamiz.
H−1AH =(
0 1
1 1)(
2 −1
1 4 )(
−1 1
1 0)=(
0+1 0+4
2+1 −1+4)(
−1 1
1 0)=¿
(
1 4
3 3)(
−1 1
1 0)=(
−1+4 1+0
−3+3 3+0)=(
3 1
0 3)= J.
Tenglamalar sistemasi umumiy yechimini quyidagi foemula orqali hisoblaymiz:
X (t)=C1eλ1tV1+C2eλ1tV2(tV1+V2)=¿C1e3t
(
−1
1 )+C2e3t
[t(
−1
1 )+(
1
0)].
1.3.4- misol. Tenglamalar sistemasini yeching.
dx
dt = − 4 x − 6 y − 6 z
,
dy
dt = x+3y+z, dz
dt = 2 x + 4 z .
Yechilishi . Xarakteristik tenglamasini tuzamiz va ildizlarini topamiz.
det ( A − λE ) =
| − 4 − λ − 6 − 6
1 3 − λ 1
2 0 4 − λ | = 0.
Determinantni uchinchi qator bo’ylab yoyamiz:
2(−6+6(3− λ))+(4− λ)((− 4− λ)(3− λ)+6)=0,
⇒ 2(− 6λ+12 )+(4− λ)(λ2+λ−6)=0,
⇒ − 12 λ + 24 + 4 λ 2
– λ 3
+ 4 λ − λ 2
− 24 + 6 λ = 0 ,
⇒ λ3− 3λ2+2λ=0,
⇒ λ ( λ − 1 ) ( λ − 2 ) = 0.
Demak, xarakteristik matritsa uchta har xil xos qiymatga ega:
λ1=0,λ2= 1,λ3= 2
.
15](/data/documents/f9a4f57c-809a-4098-9e05-265d5d0a876d/page_15.png)


![V13=−V33=−t,⇒ V23=V33+V13=0.bundan,
V
3 =
( V
13
V
23
V
33 ) = ( − t
0
t ) = t ( − 1
0
1 ) ∽ ( − 1
0
1 ) ,
V
3 xos vektorni to’g’riligini xos qiymat ta’rifidan foydalanib tekshiramiz.
A V
3 =
( − 4 − 6 − 6
1 3 1
2 0 4 )( − 1
0
1 ) = ( 4 + 0 − 6
− 1 + 0 + 1
− 2 + 0 + 4 ) = ( − 2
0
2 ) = 2 ( − 1
0
1 ) = λ
3 V
3 .
Demak, barcha xos vektorlar topildi. Endi, tenglamalar sistemasi umumiy
yechimini quyidagicha holatda bo’ladi:
X (t)=(
x
y
z)=∑i=1
3
CieλitVi=C1(
−6
1
3 )+C2et
(
− 6
1
4 )+C3e2t
(
−1
0
1 ).
1.3.5-misol. Tenglamalar sistemasi umumiy yechimini toping.
dx
dt = x − y − z
, dy
dt = − x + y − z ,
dz
dt = − x − y + z .
Yechilishi . Tenglamalar sistemasiniing xarakteristik tenglamasini tuzamiz va
ildizlarini topamiz.
det ( A − λE ) =
| 1 − λ − 1 − 1
− 1 1 − λ − 1
− 1 − 1 1 − λ | = 0 , ⇒
( 1 − λ )[( 1 − λ ) 2
− 1 ] + 1 ∗ ¿
¿
⇒ λ 2
-2λ- λ 3
+2λ 2
+2λ-4=0, ⇒ λ 3
-3λ 2
+4=0
Ko’rish mumkinki, kubik tenglama bitta ildizi
λ=−1 . Shuning uchun,
tenglamadan ( λ + 1 )
ko’paytuvchi ajratamiz, u holatda:
λ 3
+ λ 2
− 4 λ 2
− 4 λ + 4 λ + 4 = 0 , ⇒ λ 2
( λ + 1 ) − 4 λ ( λ + 1 ) + 4 ( λ + 1 ) = 0 ,
⇒ (λ+1)(λ2−4λ+4)=0,⇒ (λ+1)(λ− 2)2=0.
Bundan ko’rinadiki, bu sistemasining ikkita xos qiymati mavjud:
λ
1 = − 1 k
1 = 1
karrali va λ
2 = 2 k
2 = 2
karrali.
Xos vektorlarni topamiz.
λ1=−1 xos son uchun matritsa rangini hisoblaymiz:
18](/data/documents/f9a4f57c-809a-4098-9e05-265d5d0a876d/page_18.png)

![Umumiy yechimning barcha komponentlarini yig’ib, bir uni quyidagi
shaklda ifodalashimiz mumkin.X (t)=C1e−t
(
1
1
1)+C2e2t
(
−1
0
1 )+C3e2t
(
−1
1
0 ).
1.3.6-misol. Tenglamalar sistemasi umumiy yechimini aniqlang.
dx
dt = − 3 x − 6 y + 6 z
,
dy
dt = x+6z, dz
dt = − y + 4 z .
Yechilishi. Tenglamalar sistemasining xarakteristik tenglamasini tuzamiz va
ildizlarini topamiz.
det ( A − λE ) =
| − 3 − λ − 6 6
1 0 − λ 6
0 − 1 4 − λ | = 0 , ⇒
( − 3 − λ ) ( ( − λ ) ( 4 − λ ) + 6 ) − 1 ∗ [ ( − 6 ) ( 4 − λ ) + 6 ] = 0 ,
⇒ (λ+3)(λ2−4λ+6)+6λ−18 =0,
⇒ λ 3
+ 3 λ 2
− 4 λ 2
− 12 λ + 6 λ + 18 + 6 λ − 18 = 0 , ⇒ λ 3
− λ 2
= 0 ,
⇒ λ 2
( λ − 1 ) = 0.
Ko’rinib turibdiki, ikkita xos qiymat mavjud.
k1= 2 karrali λ1=0 va k2=1
karrali
λ2=1 xos qiymatlar mavjud.
(
A − λ
1 E )
matritsa rangini hisoblaymiz:
(
A − λ
1 E ) = ( − 3 − 6 6
1 0 0
0 − 1 4 )| − 1
3
¿ ∽ ( 1 2 − 2
1 0 6
0 − 1 4 ) ¿
∽
( 1 2 − 2
0 − 2 8
0 − 1 4 ) ∽
(
1 2 −2
0 −1 4 )
.
Demak, rank
( A − λ
1 E ) = 2
va shunga mos ravishda xos qiymatning geometrik
karralisi
s1λ1=0 da quyidagicha:
s
1 = n − rank ( A − λ
1 E ) = 3 − 2 = 1
.
20](/data/documents/f9a4f57c-809a-4098-9e05-265d5d0a876d/page_20.png)



![X ( t ) =( x
y
z ) = C
1 e λ
1 t
V
1 + C
2 e λ
1 t
( V
1 t + V
2 ) + C
3 e λ
2 t
V
3 = ¿
= C
1
( − 6
4
1 ) + C
2 [ t( − 6
4
1 ) + ( 4
− 1
0 )] + C
3 e t ( − 3
3
1 ) .
1.3.7- misol. Chiziqli differensial tenglamalar sistemasining umumiy
yechimini toping:
dx
dt = 4 x + 6 y − 15 z
, dy
dt = x + 3 y − 5 z ,
dz
dt = x + 2 y − 4 z .
Yechilishi . Tenglamalar sisteamsi xarakteristik tenglamasini tuzamiz va xos
qiymatlarini aniqlaymiz.
det (A− λE )=|
4− λ 6 −15
1 3− λ −5
1 2 − 4− λ|= 0,⇒
(4− λ)¿
⇒ (4− λ)(λ2+λ− 2)−(−6λ+6)+(15 −15 λ)=0,
⇒ 4 λ 2
− λ 3
+ 4 λ − λ 2
− 8 + 2 λ + 6 λ − 6 + 15 − 15 λ = 0 ,
⇒ λ3− 3λ2+3λ−1=0,⇒ (λ−1)3= 0.
Tenglama
k1= 3 karrali λ1=1 xos qiymatga ega ekanligiga erishamiz.
( A − λE )
matritsa rangini hisoblaymiz.
(
4 − 1 6 − 15
1 3 − 1 − 5
1 2 − 4 − 1 ) ∽ ( 3 6 − 15
1 2 − 5
1 2 − 5 ) ∽
( 1 2 − 5 ) .
Matritsa rangi 1 ga teng. Endi λ
1 = 1
xos qiymat uchun geometrik karralisini
topamiz.
s
1 = n − rank ( A − λ
1 E ) = 3 − 1 = 2
.
Bundan kelib chiqadiki, Jordan formasi ikkita Jordan katagidan iborat. Ya’ni,
7-holatga mos keladi.
λ1=1 xos qiymat uchun V1 va V2 xos vektorlar qidiramiz. V1 vektor
koordinatalarini
V1=(V11,V21,V31)T ko’rinishda olamiz. Tenglamani yechamiz.
24](/data/documents/f9a4f57c-809a-4098-9e05-265d5d0a876d/page_24.png)

![Topilgan U 1 vektorni (A− λ1E) operatorining yadrosiga tegishli ekanligini
tekshiramiz, ya’ni, A matritsaning xos vektori:
(A− λ1E)U 1
= ( 3 6 − 15
1 2 − 5
1 2 − 5 )( 3
1
1 ) = ¿
(
9+6−15
3+2−5
3+2−5)=(
0
0
0)= 0.
Shunday qilib, 2x2 Jordan katakchasi bilan bog’langan ikkita
U 1 va U
2 bazis
vektorlarni aniqladik. Yana 1x1 elementar katakda yana bitta xos vektor mavjud
bo’lib, u A matritsasining
U 1=(3,1,1 )T vektoriga kolinear bo’lmagan har qanday
xos vektor sifatida qabul qilinishi mumkin. Masalan, yechim boshida topilgan
V
2 = ( 5,0,1 ) T
vektorni olaylik.
Hisoblangan uchta chiziqli erkli vektor
U 1, U 2 va V2 Jordan bazisini tashkil
qiladi. Tenglamalar sistemasi umumiy yechimi quyidagicha ko’rinishda bo’ladi.
X
( t) =
( x
y
z ) = C
1 e λ
1 t
U
1 + C
2 e λ
1 t (
t U
1 + U
2 ) + C
3 e λ
1 t
V
2 =
=C
1 e t
( 3
1
1 ) + C
2 e t [
t( 3
1
1 ) + ( 1
0
0 )] + C
3 e t ( 5
0
1 )
1.3.8-misol. Tenglamalar sistemasining umumiy yechimini toping
dx
dt =−7x−5y−3z
, dy
dt = 2 x − 2 y − 3 z ,
dz
dt = y .
Yechilishi. Tenglamlar sistemasining xarakteristik tenglamasini tuzamiz va
ildizlarini topamiz.
det ( A − λE ) =
| − 7 − λ − 5 − 3
2 − 2 − λ − 3
0 1 − λ | = 0 ,
⇒ ( − 7 − λ ) [ ( − 2 − λ ) ( − λ ) + 3 ] − 2 ( 5 λ + 3 ) = 0 ,
⇒ ( λ + 7 ) ( λ 2
+ 2 λ + 3 ) + 10 λ + 6 = 0 ,
⇒ λ3+7λ2+2λ2+14 λ+3λ+21 +10 λ+6=0,
⇒ λ 3
+ 9 λ 2
+ 27 λ + 27 = 0 ,
⇒ ( λ + 3 ) 3
= 0.
26](/data/documents/f9a4f57c-809a-4098-9e05-265d5d0a876d/page_26.png)


![H−1 teskari matritsasi esa quyidagiga teng:
H − 1
=
( 0 0 1
2
0 1
2 3
2
1 2 3 ) ,
Matritsalarni tenglamaga qo’yib quyidagiga erishamiz:
H−1AH =
(
0 0 1
2
0 1
2
3
2
1 2 3
)(
−7 −5 −3
2 −2 −3
0 1 0 )(
6 − 4 1
−6 2 0
2 0 0)=¿
¿
( 0 1
2 0
1 1
2 − 3
2
− 3 − 6 − 9 )( 6 − 4 1
− 6 2 0
2 0 0 ) = ( − 3 1 0
0 − 3 1
0 0 − 3 ) = J .
Natijada biz Jordan formasida bitta 3x3 Jordan katagini topamiz.
Tenglamalar sistemasi umumiy yechimi esa quyidagi ko’rinishda bo’ladi:
X ( t ) = C
1 e λ
1 t
V
1 + C
2 e λ
1 t
( V
1 t + V
2 ) + C
3 e λ
1 t
( t 2
2 ! V
1 + t V
2 + V
3 ) = ¿
=C
1 e -3t
( 6
− 6
2 ) − C
2 e − 3 t [
t( 6
− 6
2 ) + ( − 4
2
0 )] + C
3 e − 3 t [ t 2
2 ( 6
− 6
2 ) + t ( − 4
2
0 ) + ( 1
0
0 )] .
II Bob. Jordan matritsasi yordamida bir jinsli chiziqli
differensial tenglamalar sistemasini yechish.
2.1-§. Ikki noma’lumli tenglamalar sistemasini yechish.
29](/data/documents/f9a4f57c-809a-4098-9e05-265d5d0a876d/page_29.png)





![(
−1 −1
1 1 ) (
−1 −1
0 0 )rank
( A − λ
1 E ) = 1 s
1 = n − rank ( A − λ
1 E ) = 2 − 1 = 1
xos vektor v
1 = ( v
11 , v
21 ) T
quyidagi tenglama orqali topiladi:
(A− λ1E)v1= 0
(
−1 −1
1 1 )(
v11
v21)=0
{
−v11−v21= 0
v11+v21=0
Agar
v21=t deb olsak, u holda v11=− v21=−t
v
1 =
( v
11
v
21 ) = ( − t
t ) t ( − 1
1 ) ( − 1
1 )
Tenglamalar sistemasi umumiy yechimini topish uchun yana bitta chiziqli erkli
xos vektor lozim. Bu vektor sifatida biz bog’langan v
2 = ( v
12 , v
22 ) T
v
ektorni olamiz
va bu vektor quyidagi tenglama orqali topiladi:
(A− λ1E)v1= v1
(
− 1 − 1
1 1 )( v
12
v
22 ) = ( − 1
1 )
{
−v12− v22=−1
v12+v22=1
v
2 =
( v
12
v
22 ) = ( 2
− 1 )
Tenglamalar sistemasi umumiy yechimini quyidagi foemula orqali hisoblaymiz:
X ( t ) = C
1 e λ
1 t
v
1 + C
2 e λ
1 t
v
2 ( t V
1 + V
2 ) = C
1 e 2 t
( − 1
1 ) + C
2 e 2 t [
t( − 1
1 ) + ( 2
− 1 )] .
2.1.6-misol . Tenglamalar sistemasini yeching.
{
˙x = 2 x
˙y = 3 y
35](/data/documents/f9a4f57c-809a-4098-9e05-265d5d0a876d/page_35.png)




![bu esa geometrik karralisi esa s2= n− rank (A− λ2E)=3− 2=1
Qolgan chiziqli erkli xos vektor v
3 bog’langan v
2 vektor orqali topiladi:
(A− λ2E)v3=v2
.
(
1 − 1 − 1
− 1 1 − 1
− 1 − 1 1 )( v
13
v
23
v
33 ) = ( 1
− 1
0 )
{
v
13 − v
23 − v
33 = 1
− v
13 + v
23 − v
33 = − 1
− v
13 − v
23 + v
33 = 0
Bundan,
v
3 =
( v
13
v
23
v
33 ) = ( 2
1
0 )
Tenglamalar sistemasi umumiy yechimi quyidagi formula bilan ifodalanadi:
X (t)=(
x
y
z)=C1eλ1tv1+C2eλ2tv2+C3eλ2t(v2t+v3)
=
= C
2 e 2 t
( 1
− 1
0 ) + C
3 e 2 t [
t( 1
− 1
0 ) + ( 2
1
0 )] + C
1 e 5 t ( − 1
3
− 1
3
1 )
2.2.9-misol .Tenglamalar sistemasini yeching.
{
˙x = − 3 x + 4 y − 2 z
˙y = x + z
˙z = 6 x − 6 y + 5 z
Yechilishi. Sistemaning xarakteritik tenglamasini tuzib, xos qiymatlarni
topamiz:
(
A − λE ) =
| − 3 − λ 4 − 2
1 − λ 1
6 − 6 5 − λ | = 0
40](/data/documents/f9a4f57c-809a-4098-9e05-265d5d0a876d/page_40.png)



![( A − λ
1 E ) v
3 = v
2( 2 − 1 0
3 − 1 − 1
1 0 − 1 )( v
13
v
23
v
33 ) = ( 1
1
0 )
{
2 v
13 − v
23 = 1
3 v
13 − v
23 − v
33 = 1
v
13 − v
33 = 0
Bu sistemada, agar, v
13 = v
33 = 1
desak u holda,
v13= v23=1, bo’ladi.
Ya’ni,
v
3 =
( v
13
v
23
v
33 ) = ( 1
1
1 )
Tenglamalar sistemasi umumiy yechimi esa quyidagi ko’rinishda
bo’ladi:
X (t)=C1eλ1tv1+C2eλ1t(v1t+v2)+C3eλ1t(t2
2!v1+tv2+v3)
=
¿ C
1 e − t
( 1
2
1 ) − C
2 e − t [
t( 1
2
1 ) + ( 1
1
0 )] + ¿
+ C
3 e − t
[ t 2
2 ( 1
2
1 ) + t ( 1
1
0 ) + ( 1
1
1 )]
2.2.11-misol . Tenglamalar sistemasi umumiy yechimini toping.
{
˙x=3x+y+y
˙y= x+3y+z
˙z= 2x− 2y+4z
Yechilishi . Tenglamalar sistemasini xarakteristik tenglamasini tuzamiz va xos
sonlarni topamiz.
(
A − λE ) = 0 , ⇒
( 3 − λ 1 1
1 3 − λ 1
2 − 2 4 − λ ) = 0
¿
λ3−10 λ2+32 λ−32 =0
λ1=2,λ2=4
44](/data/documents/f9a4f57c-809a-4098-9e05-265d5d0a876d/page_44.png)

![v
2 =( v
12
v
22
v
32 ) = ( t
t
0 ) t ( 1
1
0 ) ( 1
1
0 )
v3
bog’langan vektorni esa quyidagi fomula orqali hisoblaymiz.
(A− λ2E)v3=v2
.
(
− 1 1 1
1 − 1 1
2 − 2 0 )( v
13
v
23
v
33 ) = ( 1
1
0 )
{
−v13+v23+v33=1
v13−v23+v33=1
2v13− 2v23=0
Yuqoridagi sistemadan v
13 = v
23 = 1
deb olsak,
v13=1 bo’ladi
Bundan,
v3=
(
v13
v23
v33)
=
(
1
1
1) (
1
1
1)
Tenglamalar sistemasi umumiy yechimi quyidagi formula bilan ifodalanadi:
X
( t) =
( x
y
z ) = C
1 e λ
1 t
v
1 + C
2 e λ
2 t
v
2 + C
3 e λ
2 t
( v
2 t + v
3 )
=
=
C1e2t
(
1
− 2
1 ) + C
2 e 4 t ( 1
1
0 ) + C
3 e 4 t [
t( 1
1
0 ) + ( 1
1
1 )] .
2.2.12-misol , Tenglamalar sistemasi umumiy yechimini toping.
{
˙x= x+2y
˙y= 2y
˙z=−2x− 2y+z
Yechilishi. Tenglamalar sistemasini xarakteristik tenglamasini tuzamiz va xos
sonlarni topamiz
(
A − λE ) = 0
46](/data/documents/f9a4f57c-809a-4098-9e05-265d5d0a876d/page_46.png)



![Bundan, yuqoridagi tenglamadan kelib chiqadiki, v22=v32=t deb olsak,
v
12 = − 2
3 v
22 = − 2
3 t
bo’ladi.
v2=
(
v12
v22
v32)
=
(
− 2
3 t
t
t )
t
(
−2
3
1
1 ) (
− 2
3
1
1 )
.
v3
bog’langan vektorni esa v2 yordamida hisoblaymiz.
(A− λ2E)v3=v2⇒ (
2 1 −1
4 4 −2
8 6 −4)(
v13
v23
v33)
=
(
−2
3
1
1 )
{
2v12+v22−v32= −2
3
3v12+4v22− 2v32=1
8v12+6v22− 4v32=1
Yuqoridagi tenglamadan
v
13 = − 0.5 , v
23 = 11
6 , v
33 = 1.5 .
Ekanligini topamiz. Ya’ni,
v
3 =
( v
13
v
23
v
33 ) = ( − 0.5
11
6
1.5 )
Tenglamalar sistemasi umumiy yechimi quyidagi formula bilan ifodalanadi:
X (t)=(
x
y
z)=C1eλ1tv1+C2eλ2tv2+C3eλ2t(v2t+v3)=¿
¿C1e3t
(
0
1
1)+C2et
(
−2
3
1
1 )
+C3et
[
t
(
− 2
3
1
1 )
+
(
−0.5
11
6
1.5 )]
.
2.2.14-misol . Tenglamalar sistemasi umumiy yechimini toping.
50](/data/documents/f9a4f57c-809a-4098-9e05-265d5d0a876d/page_50.png)

![(A− λ2E)v2=0⇒
(
−5 2 5
6 − 2 −6
−8 3 8 )(
v12
v22
v32)
=0
{− 5 v
12 + 2 v
22 − 5 v
32 = 0
6 v
12 − 2 v
22 − 6 v
32 = 0
− 8 v
12 + 3 v
22 + 8 v
32 = 0
Bundan, yuqoridagi tenglamadan kelib chiqadiki,
v12= v32=t deb olsak, v22=0
bo’ladi.
v2=
(
v12
v22
v32)
=
(
t
0
t)
t
(
1
0
1) (
1
0
1)
.
v
3
bog’langan vektorni esa v
2 yordamida hisoblaymiz.
( A − λ
2 E ) v
2 = v
2 ⇒
( − 5 2 5
6 − 2 − 6
− 8 3 8 )( v
13
v
23
v
33 ) = ( 1
0
1 )
{
− 5 v
12 + 2 v
22 − 5 v
32 = 1
6 v
12 − 2 v
22 − 6 v
32 = 0
− 8 v
12 + 3 v
22 + 8 v
32 = 1
Yuqoridagi tenglamadan
v13=−11 ,v23=−30 ,v33=1.
Ekanligini topamiz. Ya’ni,
v
3 =
( v
13
v
23
v
33 ) = ( − 11
− 30
1 )
Tenglamalar sistemasi umumiy yechimi quyidagi formula bilan ifodalanadi:
X (t)=(
x
y
z)=C1eλ1tv1+C2eλ2tv2+C3eλ2t(v2t+v3)=¿
¿ C
1 e 2 t
( 5.5
1
5 ) + C
2 e t ( 5.5
1
5 ) + C
3 e t [
t( 5.5
1
5 ) + ( − 11
− 30
1 )] .
52](/data/documents/f9a4f57c-809a-4098-9e05-265d5d0a876d/page_52.png)



Chiziqli differensial tenglamalar sistemasini matritsaviy usulda yechish MUNDARIJA Kirish......................................................................... 3 I Bob. Differensial tenglamalar sistemasining umumiy yechimini Jordan formasi yordamida topish. 1.1-§. Matritsaning Jordan formasi................................................5 1.2-§. Xos vektorlar va Jordan zanjiri............................................6 1.3-§. Xos vektor va mos yechimlarni topish..................................8 II Bob. Jordan matritsasi yordamida bir jinsli chiziqli differensial tenglamalar sistemasini yechish. 2.1-§. Ikki noma’lumli tenglamalar sistemasini yechish...............31 2.2-§. Uch noma’lumli tenglamalar sistemasini yechish................39 Xulosa ........................................................................ 54 Foydalanilgan adabiyotlar........................................ 55 1
Kirish Masalaning qo’yilishi. Differensial tenglamlar sistemasining umumiy yechimini Jordan formasi yordamida topish yo’llari o’rganilgan. Mavzuning dolzarbligi. Differensial tenglamalar sistemasiga oida masalalar yechishda algebraik usullarni qo’llash. Xususan, Jordan matritsasini qo’llash. Ishning maqsad va vazifalari. Malakaviy bitiruv ishining maqsadi ikkinchi va uchinchi tartibli Jordan matritsalarni Jordan normal formasiga keltirish va shu matritsalar yordamida diffferensial tenglamalar sistemasi umumiy yechimlarini topish yo’lining umumiyrroq usuli, Jordan normal formasiga keltirish yordamida barcha holatlar ko’rib chiqilgan. Ilmiy tadqiqot usullari. Algebraik usullar yordamida chiziqli differensial tenglamalar sistemasini topish. Ishning amaliy ahamiyati. Mazkur ishdan bakalavr yo’nalishi ikkinchi kurs talabalari o’zgarmas koeffisiyentli chiziqli differensial tenglamalar sisteamsini yechimini topishda foydalanilishi mumkin. Ishning tuzilishi. Malakaviy bitiruv ishi kirish qismi, ikkkita bob, xilosa va foydalanilgan adabiyotlardan tshkil topgan. Kirish qismida masalaning masalaning qo’yilishi, mavzuning dolzarbligi, maqsad va vazifalari hamda, olingan natijalar haqida so’z yuritiladi. Birinchi bobda, differensial tenglamalar sistemasi umumiy yechimini topishda,yechimni Jordan formasi yordamida topish usuli barcha holatlari hamda, Jordan normal formasi, Jordan bazisi haqida va xos sonlarning barcha karrali va karrali bo’lmagan, holatlari bayon etilgan Ikkinchi bobda, differensial tenglamalar sistemasi umumiy yechimini Jordan formasi orqali topish usuli barcha holatlari. Xususan, xos son karrali 2
bo’lgan va bo’lmagan barcha holatlari uchun misollar yechimlari ko’rsatilib o’tilgan. 3
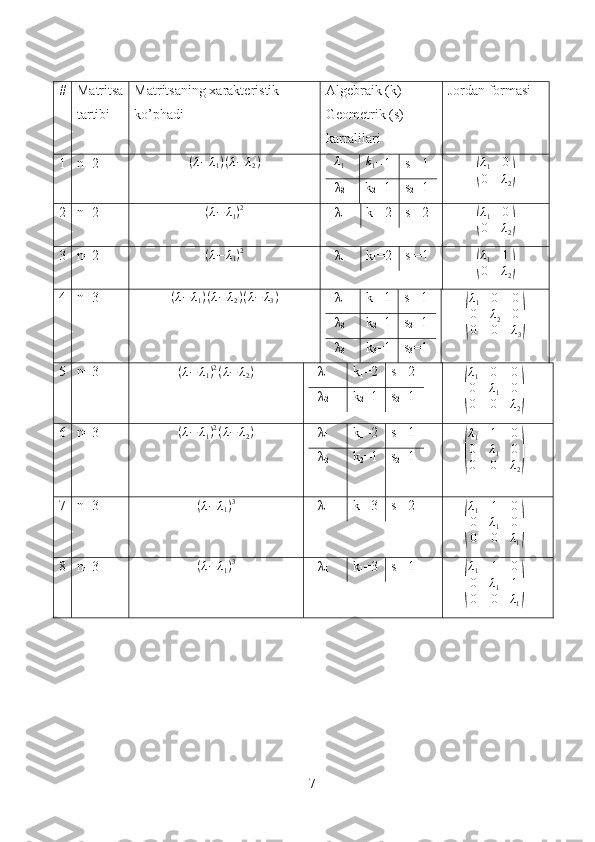
I Bob. Differensial tenglamalar sistemasining umumiy yechimini Jordan formasi yordamida topish O’zgarmas koeffisientli n- tartibli bir jinsli chiziqli differensial tenglamalar ko’rib chiqaylik.X'(t)= AX (t) Bunda X ( t) = ( x 1 ( t ) x 2 ( t) . . x n ( t ) ) , A = ( a 11 a 12 … a 1 n a 21 a 22 … a 2 n … … … … a n 1 a n 2 … a nn ) . Bunday sistemaning umumiy yechimlar sistemasi n ta chiziqli funksiyani o’z ichiga olishi kerak. Xos sonlar va xos vektorlar usulidan foydalangan holatda yechimni topishda ko’p holatlarda xos vektorlar soni n dan kam ekanligi ma’lum bo’ladi. Ya’ni, shunday sistemalar borki, ular uchun faqat xos vektorlardan iborat bazis mavjud emas. Bunday holatda yechimni boshqa usul bilan, masalan, aniqmas koeffisiyentlar usuli yordamida topish mumkin. Biroq, umumiy yechimni topishning umumiyroq va isbotlangan usuli mavjud. Bu har qanday kvadrat matritsani Jordan normal formasi deb ataladigan formaga keltirish usulidir. (umuman olganda, bu kompleks maydonga to’g’ri keladi.) Matritsaning Jordan formasini va Jordan bazisini bilgan holatda, tenglamalarning sistemasining umumiy yechimini korsatish mumkin. Ushbu yechim yo’lini batafsil ko’rib chiqaylik. Buning uchun oldin ba’zi asosiy ta’riflarni keltiramiz. 1.1-§. Matritsaning Jordan formasi . Jordan formasi kvadrat matritsa bosh diagonali orqali ifodalaniladi. Matritsa bosh diagonali bo’ylab esa Jordan katagi deb ataluvchi matritsa joylashgan bo’lib, xos sonlari bilan mos tushadi. Bosh diagonaldagi λ i lar mos ravishda 4
Jordan kataglaridan iborat bo’lib, kataklar joylashishi λ i lar bog’liq emas. Quyida Jordan matrisa umumiy ko’rinishini ko’rishimiz mumkin. J =( λ 1 1 0 0 0 0 0 λ 1 0 0 0 0 0 0 λ 2 0 0 0 0 0 0 λ 3 1 0 0 0 0 0 λ 3 1 0 0 0 0 0 λ 3 ) . Matritsada 3 xil Jordan kataklariga mos keladigan matritsa elementlari turli xil rangda ko’rsatilgan. Bundan tashqari bu matritsada λ3 matritsaning xos qiymatlari bosh diagonalda bo’ladi va har bir xos qiymat λ 3 ning algebraik ko’phadi ki marta uchraydi. 1 dan katta har bir Jordan katagi mavjud bosh diagonal ustidagi parallel qator birlardan iborat bo’lib, Jordan matritsasining boshqa barcha elementlari nolga teng. Jordan kataklarining matritsada joylashish tartibi aniq belgilanganmagan. 1.2-§. Xos vektorlar va Jordan zanjiri Xos qiymati λ bo’lgan k o’lchamdagi Jordan katakchasini ko’rib chiqaylik. Bunda Jordan katagi bazis vektorlari : V 1 V 2 ... V n . V 1 ( V 1 ≠ 0 ) v ektorlar xos vektor bo’lib, ular mos matritsalarni qanoatlantiradi. AV1= λV1⇒ (A− λE )V1=0 Yuqoridagi tenglamadan esa V2(V2≠0) ekanligi kelib chiqadi. (A− λE )V2=V1 Yuqoridagi vektor esa birinchi tartibli bog’langan vektor deyiladi. Xuddi shunday yuqori tartibli boshqa bog’langan vektorlarini topamiz. (A− λE )V3=V2 .................... ( A − λE ) V k = V k − 1 Bu munosabatlardan quyidagilarga ega bo’lamiz: (A− λE )V1=0 va (A− λE )V2=V1 Bu tengliklardan esa quyidagiga kelamiz: (A− λE )2V2=0 5
