logo
  1. Bosh sahifa
  2. Diplom ishlar
  3. Umumiy
  4. DEFORMATSIYALANUVCHI MUHITDA JOYLASHGAN SILINDRIK QOBIQNING BURALMA TEBRANISHLARIGA AYLANISH INERSIYASI VA KO’NDALANG SILJISH DEFORMATSIYASI TA’SIRI

DEFORMATSIYALANUVCHI MUHITDA JOYLASHGAN SILINDRIK QOBIQNING BURALMA TEBRANISHLARIGA AYLANISH INERSIYASI VA KO’NDALANG SILJISH DEFORMATSIYASI TA’SIRI

Yuklangan vaqt:

12.08.2023

Ko'chirishlar soni:

0

Hajmi:

1907 KB
Ko'chirib olish
DEFORMATSIYALANUVCHI MUHITDA JOYLASHGAN SILINDRIK QOBIQNING BURALMA TEBRANISHLARIGA AYLANISH INERSIYASI VA KO’NDALANG SILJISH DEFORMATSIYASI TA’SIRI MUNDARIJA KIRISH........................................................................... ...............3 I-BOB. DOIRAVIY ELASTIK STERJEN BURALMA TEBRANISHI ASOSIY TENGLAMALARI. §1.1 Doiraviy elastik silindrik sterjenning vaqtdan bog’liq tebranishlari .................................................................................9 §1.2 Doiraviy elastik silindrik sterjenning buralma tebranishi umumiy tenglamalari.................................................................................16 §1.3 Doiraviy silindrik qobiqning buralma tebranishlarida deformarsiyalanuvchi muhit ta’sirini e’tiborga olish..................26 §1.4 Doiraviy elastik silindrik sterjenning buralma tebranishlari asosiy tenglamalari (xususiy hol)...........................................................33 II-BOB DIFFERENSIAL TENGLAMALARNI YECHISHNING SONLI USULLARI §2.1 С hekli ayirmalar usulini d ifferentsial tenglamalar yechishda qo’llanilishi..................................................................................37 §2.2 Differentsial tenglamalarni taqribiy yechish ….........................45 III-BOB DOIRAVIY ELASTIK SILINDRIK QOBIQNING BURALMA TEBRANISHLARI §3.1 Doiraviy elastik silindrik qobiqning buralma tebranish tenglamalarida aylanish inersiyasi ta’siri ...................................51 §3.2 Doiraviy elastik silindrik qobiqning buralma tebranish tenglamalarida ko’ndalang siljish deformatsiyasi ta’siri............................................................................................58 XULOSA…...………..…………………………………………60 FOYDALANILGAN ADABIYOTLAR RO’YXATI……….....61 Ilovalar.........................................................................................64 Kirish Keyingi vaqtlarda fan va texnikaning jadal rivojlanishi turli xil yangi t urdagi konstruksiya elementlarini yangi tex nologiyalar asosida yaratishga olib kelmoqda. Hozirgi zamon texnikasi tez sur’atlar bilan rivojlanishi mexanika sohasida qilinishi kerak bo’lgan yangidan-yangi, nazariy va amaliy masalalarni yechishni qo’ymoqda. Keyingi yillarda materiallar yuqori bosimli va yuqori haroratli o’ta murakkab jarayonlarda qo’llanilmoqda. Materiallar chidamli, mustahkam va arzon bo’lishi uchun ularning qotishmalaridan o’ta mustahkam va yaroqli modulli tolalar amaliyotda keng qo’llanilmoqda. Bunday yangiliklar jismning elastiklik modeli bilan bir qatorda, deformatsiyalanuvchi qattiq jismning boshqa, umumiyroq va mukammalroq modellarini ham yaratishga olib keldi va bu modellardan keng miqyosda foydalanilmoqda. Bunda jismlarning plastiklik, qovushoq-elastiklik xususiyatlaridan keng ko’lamda foydalanishga olib kelmoqda. Keyingi yillar davomida deformatsiyalanuvchi qattiq jismlar mexanikasining “yemirilish mexanikasi”, “kompozit materiallar mexanikasi”, “Nanomexanika” va shu kabi qator yangi yo’nalishlar paydo bo’lishiga ham ana shu yangi talablar sabab bo’ladi. Ushbu yangiliklar zamirida eng avvalo elastik jism modeli yotadi. Dissertatsiya ishining tadqiqot predmeti t ashqi ta’sir natijasida konstrukksiya elementlari sterjenlar, plastinka va qobiqlarda paydo bo’ladigan tebranish turlarini aniqlash. Tebranishlar vaqtdan bog’liq xususiyatga ega bo’lgan hollarda bunday elementlarda paydo bo’ladigan nostatsionar to’lqinlar tarqalish jarayonlarini, ularning fizik-mexanik xususiyatlarini hisobga olgan holda tadqiq qilishdan iborat. Vaqtdan bog’liq tebranishlarni o’rganishda tebranishlarning xususiy chastotalari, xususiy amplitudalarini aniqlash va tebranish formalarini topish masalalarini qo’yish, ularni yechish va ilmiy xulosalar chiqarish. 2 Qobiqlarlar nostatsionar tebranishlarni tashqi dinamik yuklar ta’sirida uyg’otilgan hollar uchun fizik-mexanik xarakteristikalardan foydalanib tadqiq etish dissertatsiya ishining predmetini tashkil etadi. Dissertatsiya ishining tadqiqot ob’ekti yuqorida aytib o’tilgan xulosalardan foydalanib, ko’ndalang kesimi doiraviy, uzunligi chekli, materiali elastik bo’lgan silindrik qobiq va qatlamlar qaralgan. Bunda qobiqlarning buralma tebranishlarida hosil bo’ladigan kuchlanganlik-deformatsiyalanganlik holatini qatlam materialining fizik-mexanik xususiyatini e’tiborga olgan holda aniqlash mumkin. Bulardan tashqari qobiqni o’rab turuvchi asosiy ob’yekt tariqasida deformatsiyalanuvchi muhit ta’siri ham e’tiborga olingan. Mavzuning dolzarbligi doiraviy elastik qobiqlar mexanika sohasining juda ko’p va xilma-xil muhandislik qurilmalari tarkibiy qismlarini tashkil qiladi.Bunday qobiq va qatlamlar ko’plab mashina va mexanizmlarning asosiy elementlari hisoblanadi. Demak o’z-o’zidan ko’rinadiki bunday qobiq va qatlamlar turli xil dinamik tashqi ta’sirlar ostida bo’ladi va ularning ko’ndalang kesimlarida har xil yuklanishlar paydo bo’ladi. Sterjenlardagi bunday yuklanishlarni aniqlash masalasi deformatsiyalanuvchi qattiq jismlar mexanikasining dolzarb masalalaridan biri hisoblanadi. Tashqi ta’sirlar ostidagi qobiq va qatlamlar ko’ndalang kesimlaridagi kuchlanganlik-deformatsiyalanganlik holatlarini aniqlash dolzarb hisoblanadi. Bunda, tashqi dinamik ta’sirlar natijasida qatlam nuqtalarida paydo bo’ladigan kuchlanganlik-deformatsiyalanganlik holatlarini aniqlash murakkablashadi. Bunday hollarda masalani analitik yechish mumkin bo’lmay qoladi va masalani yechishda sonli usullardan foydalanishga to’g’ri keladi. Shulardan kelib chiqqan holda dissertatsiya doirasida qaralgan masala dolzarb masalalar qatoriga kiradi deb hisoblash mumkin. Deformatsiyalanuvchi qattiq jismlar mexanikasi masalalarini sonli yechishda qo’llanilib kelinayotgan usullardan chekli elementlar, chekli ayirmalar va chegaraviy elementlar usullarini keltirishimiz mumkin. Bunday usullardan biri sifatida dissertatsiya doirasida chekli ayirmalar usulidan foydalanamiz. Bundan 3 tashqari qaralayotgan masalalarni yechishda ularning matematik modelini qurishda asosiy omil sidatida [1, 2] ishlarining natijalaridan foydalanamiz. Ishning maqsad va vazifalari magistrlik dissertatsiyasi ishining asosiy maqsadi qilib ko’ndalang kesimi doiraviy bo’lgan elastik silindrik qobiq va qatlamlarning vaqtdan bog’liq buralma tebranishlarini tadqiq qilish, tenglamalarda aylanish inersiyasi hamda ko’ndalang siljish deformatsiyasi ta’sirlarini inobatga olish etib belgilangan. Bunda tadqiqotni klassik va aniqlashtirilgan [3,4] tebranish tenglamalari asosida olib borish va masalalarni sonli usullar yordamida yechish vazifasi qo’yilgan. Yuqorida keltirib o’tilganlardan kelib chiqib dissertatsiya ishining asosiy vazifalari qilib quyidagilar belgilangan:  elastiklik nazariyasi asosiy tenglama va munosabatlarini tahlil qilish;  ko’ndalang kesimi doiraviy elastik qobiq va qatlamlar uchun buralma tebranish umumiy tenglamalarini keltirib chiqarish;  klassik va aniqlashtirilgan tebranish tenglamalarini xususiy hollarda keltirib chiqarish;  differensial tenglamalarni yechishning sonli usullarinini tahlil qilish;  chekli ayirmalar va progonka usullarini o’rganish hamda amaliy masalalar yechishga tadbiq etish;  Olingan natijalar asosida ilmiy xulosalar chiqarish. Muammoning ishlab chiqilish darajasi. Doiraviy elastik sterjen va qobiqlarda buralma tebranishlarni tadqiq etish masalasi bilan juda ko’p olimlar shug’illanishgan va hozirgacha ilmiy izlanishlar olib borishmoqdalar. Fan va texnikaning taraqqiyot darajasi materiallarning yangidan-yangi xususiyatlarini, jumladan: reologik, anizotropik, temperaturaviy va h.k. xususiyatlarini inobatga olgan holda tadqiqotlar olib borishni talab etmoqda. Bundan tashqari sterjenlardagi buralma tebranishlarni yangi aniqlashtirilgan tebranish tenglamalar asosida keltirib chiqarish bo’yicha juda kam ishlar bajarilgan. Tadqiqotning ilmiy yangiligi. Doiraviy elastik silindrik qobiqlarning buralma tebranishlari haqidagi masalalar analitik yechimlar asosida tadqiq etilgan. 4 Aslida dinamik jarayonlarda bu kabi yechimlarni olish juda murakkab hisoblanadi. Bunda ko’proq xotira effektini hisobga oladigan aniqroq ravishda natija beradigan singulyar yadrolardan foydalaniladi. Bu kabi yadrolar bilan esa masalani analitik yechish qiyinlashadi yoki masalani yechib bo’lmaydi. Shuning uchun sterjen va qobiqlarning buralma tebranishlari haqidagi masalalarni sonli tadqiq etish talab etiladi. Sonli usullardan foydalanish hozirgi vaqtla katta ilmiy va amaliy ahamiyatga ega bo’lmoqda. Maskur dissertatsiya ishi doirasida qaralgan va yechilishi uchun sonli usullar tadbiq etilgan masalalarning ilmiy ahamiyati birinchidan, materialning elastiklik xususiyati hisobga olinganligi ikkinchidan, masalani yechish uchun chekli ayirmalar usulining qo’llanilishidan iboratdir. Dissertatsiya ishining ilmiy yangiligi doiraviy elastik qobiqning buralma tebranishi uchun tebranish tenglamalariga sonli usullarning qo’llanilishidan iboratdir. Tadqiqotning amaliy ahamiyati. Hozirgi zamon texnikasi, yer osti va yer usti inshootlari, qurilish, aviatsiya, kemasozlik va boshqa juda ko’plab sohalarda ko’ndalang kesimi doiraviy bo’lgan qobiq va qatlamlar muhandislik qurilmalarining asosiy elementlaridan biri sifatida ishlatiladi. Qo’llanilish jarayonida bunday qatlamlar intensiv va impulsli dinamik yuklar ta’siri ostida bo’ladilar. Ko’p hollarda ularning dinamik chidamlilik darajasini tajribadan emas, balki hisoblash ishlari yordamida aniqlashga to’g’ri keladi. Yuqorida keltirilganlar elastik doiraviy qatlamlarning vaqtdan bog’liq tebranishlarini tadqiq qilish, ularning tebranish chastotasi va amplitudasi, tebranishlar shakli, ko’chishi va kuchlanishi kabi boshqa xarakteristikalarini aniqlash tadqiqotning amaliy ahamiyatga ega ekanligidan dalolatdir. Dissertatsiya ishida qaralgan qobiq va qatlamlarning buralma tebranishlari haqidagi masalalar ham shunday tadqiqotlar sarasiga kiradi va muhim amaliy ahamiyatga ega bo’lgan masalalardan biri ekanligini ko’rsatadi. Dissertatsiya ishining tuzilishi. Ushbu magistrlik dissertatsiyasi ishi kirish, uchta bob, xulosa va foydalanilgan asosiy adabiyotlar ro’yxatidan iborat bo’lib jami … .betni tashkil qiladi. 5 Dissertatsiya asosiy bo’limlarining qisqacha mazmuni. Dissertatsiya ishining kirish qismida ishning predmeti va dolzarbligiga atroflicha to’xtalib o’tilgan. Ishning predmeti ishonarli qilib keltirilgan va shu asosda uning ob’yekti aniqlashtirilgan. Doiraviy elastik sterjen, qobiq va qatlamlarning buralma tebranishlarini klassik va aniqlashtirilgan tenglamalar asosida tadqiq qilish mexanikaning dolzarb mavzularidan biri ekanligi keltirilgan. Dissertatsiya ishining maqsadi va vazifalari belgilab olingan. Bunday vazifalardan bir nechtasi alohida ajratilgan va sanab o’tilgan. Ularning har biriga tavsif keltirilgan. Dissertatsiya ishida hal qilinishi kerak bo’lgan muammo tahlil qilingan. Olingan natijalarning ilmiy va amaliy ahamiyatlari aniq misollarda sodda qilib bayon etilgan. Dissertatsiya ishining birinchi bobi “Doiraviy elastik sterjenning buralma tebranishi asosiy tenglamalari” deb nomlangan va o’z ichiga to’rtta paragrafni olgan. Birinchi paragrafda d oiraviy elastik silindrik sterjenning vaqtdan bog’liq tebranishlariga doir o’tkazilgan ilmiy tadqiqot ishlariga qisqacha sharh berilgan. Ikkinchi paragrafda ko’ndalang kesimi d oiraviy elastik silindrik sterjenning buralma tebranishi umumiy tenglamalari keltirib chiqilgan va boshqa mualliflar tomonidan chiqarilgan tenglamalar bilan taqqoslash ishlari bajarilgan. Uchinchi paragraf d oiraviy silindrik qobiqning buralma tebranishlarida deformarsiyalanuvchi muhit ta’sirini e’tiborga olish deb nomlangan va qobiqni o’rab turuvchi muhitga baho berilgan. To’rtinchi paragraf d oiraviy elastik silindrik sterjenning buralma tebranishlari asosiy tenglamalari (xususiy hol) qarab chiqilgan. Aniqlashtirilgan tenglamalarning har bir hadi qanday mexanik ma’noga ega ekanligi bayon etilgan. Dissertatsiya ishining ikkinchi bobi d ifferentsial tenglamalarni yechishning chekli ayirmalar usuli, x ususiy hosilali differentsial tenglamalarni taqribiy yechish ga qo’llaniladigan asosiy formilalar keltirib chiqarishga bag’ishlangan. Shu bobning birinchi paragrafi d ifferentsial tenglamalarni yechishning chekli ayirmalar usuli deb nomlangan bo’lib bunda o’ng, chap va markaziy ayirmalar haqida 6 ma’lumotlar berilgan. Shu bobning ikkinchi paragrafida x ususiy hosilali differentsial tenglamalarni taqribiy yechish uchun asosiy formula va munosabatlar va tenglamalarni yechish tartibi keltirilgan. Keyyinchalik ushbu bobda keltirilgan ma’lumotlardan foydalanib dissertatsiya ishi doirasida aniq amaliy masalalarni yechishda uchun sonli usullardan, xususan chekli ayirmalar usulidan foydalanilgan. Dissertatsiya ishining uchinchi bobi “Doiraviy elastik silindrik qobiqning buralma tebranishlari” deb nomlangan. Bob ikkita paragrafdan iborat bo’lib birinchi paragrafda d oiraviy elastik silindrik qobiqning buralma tebranish tenglamalarida aylanish inersiyasi ta’sirini e’tiborga olish deb nomlangan. Tenglamalarda ushbu ta’sirni hisobga olgan holda uzunligi chekli bo’lgan qobiq uchun sonli natijalar olingan va grafiklar ko’rinishida tasvirlangan. Ikkinchi paragrafda d oiraviy elastik silindrik qobiqning buralma tebranish tenglamalarida ko’ndalang siljish deformatsiyasi ta’sirini e’tiborga olib uzunligi chekli bo’lgan qobiq uchun sonli natijalar olingan. K o’chishlarni vaqtdan va koordinatadan bog’liq bo’lgan grafiklari keltirilgan. Sonli natijalar asosida mexanik xulosalar chiqarilgan. 7 I-BOB. DOIRAVIY ELASTIK STERJEN BURALMA TEBRANISHI ASOSIY TENGLAMALARI §1.1 Doiraviy elastik silindrik sterjenning vaqtdan bog’liq tebranishlari Egilishning differensial munosabatlarini Bernulli statik holda chiqargunga qadar sterjenlarning egilishi haqidagi tadqiqotlar nashr qilinmagan edi. Bu tadqiqotlarni keyinchalik L.Eyler (1744) davom ettirdi. Ushbu tebranish tenglamasi o’zida inersiya kuchini hisobga oluvchi dinamik had orqali to’ldirildi va balkaning ko’ndalang tebranishi differensial tenglamasi hosil qilindi. Bu chiqarilgan tenglamalar Eyler-Bernulli tenglamalari deb nom oldi. Bizga ma’lumki, uzunligi bo’yicha bir jinsli bo’lmagan balkaning differensial tebranish tenglamasi quyidagicha ko’rinishida bo’ladi (1.1) (1.2) Bu yerda x- bo’ylama koordinata, t-vaqt, -qaralayotgan sterjen nuqtasining markaziy o’qidan chetlashishi, -eguvchi moment, -qirquvchi (ko’ndalang) kuch, - tekis taqsimlangan kuch, -sterjen ko’ndalang kesim yuzi, - Elastiklik moduli, -material zichligi. Sterjen klassik egilish tenglamalari tekis kesimlar gipotezasi (D.Bernulli gipotezasi)ga asoslangan: deformatsiyagacha tekis bo’lgan kesimlar deformatsiyadan keyin ham tekisligicha qoladi. Ko’ndalang va bo’ylama tolalar bo’yicha kuchlanishlar juda kichik, shuning uchun ularni hisobga olmasa ham bo’ladi. Tekis kesimlar gipotezasi barcha sterjenlar uchun tajribalardan katta aniqlikka ega ekanligini ko’rsatadi. Ko’pgina materiallar uchun Puasson koeffisiyenti noldan farqli bo’lgani uchun uning ta’siri bo’ylama cho’zilishda yon tomondan siqilishga, bo’ylama siqilishda esa yon tomondan kengayishga olib kelishini ko’rish mumkin. Bundan ko’rinadiki D.Bernulli gipotezasi egilish vaqtida ko’ndalang kesimdagi nuqtalarning ko’chishini cheklamaydi. Hosil qilingan (1.1) tenglamadan sterjenning tebranish tadqiqotlarida J.Fure, J.Bussinesk va boshqa olimlar 8 keyinchalik foydalanganlar. Birinchilardan bo’lib sterjenning ko’ndalang tebranishi nazariyasiga, sterjen elementlarida aylanish inersiyasi va ko’ndalang siljish deformatsiyasi ta’sirini hisobga olishni S.P.Timoshenko taklif etgan. Sterjen statik egilganda keltirilgan yechimlar ko’ndalang siljish deformatsiyasi ta’siri juda muhim ekanligini ko’rsatadi. Statik holatda ko’ndalang siljish deformatsiyasi ta’sirini bir qancha materiallarda, jumladan rezinali sterjenlarda yaqqol ko’rish mumkin [7]. Siljish deformasiyasi ta’siri yassi ko’ndalang kesimning buzilishiga sabab bo’lishi mumkin (jamlangan kuchlar, jamlangan massalar, qattiqlik yoki zichlik sakrashlari va h.k.). Bundan tashqari dinamik masalalarda tebranish modellari bilan bog’liq ko’ndalang kesimlarining tuzilishi mumkinligini aytib o’tish mumkin; vaqt bo’yicha o’zgaruvchilar, maydonlar katta gradiyentlar chegaralarida elastiklik nazariyasi klassik modellari to’g’ri kelmasligi mumkin. S.P.Timoshenko yaxlit sterjen tebranishlari haqidagi masalani qarab, past chastotalarda ko’ndalang kesim deformatsiyasining kichik ta’siri chastotaning oshishi bilan ortib boradi degan xulosaga kelgan. Bu esa uzunlik birligiga mos keluvchi buralish to’lqinlari sonining ortishini ko’rsatadi. [21] ishlariga tayanib, aylanish inersiyasi va ko’ndalang siljish deformasiyasi ta’sirini e’tiborga olib, bir jinsli prizmatik sterjen uchun buralma tebranish to’lqin tenglamasini keltiramiz. Urinmaning egrilik chizig’iga og’ish burchagi , deb olamiz, u holda buralma deformasiya, egrilik va neytral o’q oldidagi siljishlardan iborat bo’ladi, ya’ni ; (1.3) -eguvchi moment va - ko’ndalang kuch ifodalari quyidagicha: ; (1.4) 9 Sterjen cheksiz kichik elementining aylanish inersiyasi hisobga olinganda chiziq tekisligiga perpendikulyar k nuqta orqali o’tuvchi o’qqa nisbatan harakat tenglamasi quyidagicha bo’ladi: ; (1.5) Qaralalayotgan elementning - o’qqa nisbatan harakat tenglamasi quyidagi ko’rinishga ega ; (1.6) (1.4) munosabatni e’tiborga olsak (1.5) va (1.6) tenglamalardan ikkita harakat differensial tenglamalarini hosil qilamiz ; (1.7) ; (1.8) Bu differensial tenglamalardan ni yo’qotib S.P.Timoshenko tomonidan yaratilgan balka egilish tenglamasiga ega bo’lamiz ; (1.9) Agar (1.9) tenglama tarkibidagi qatnashgan hadni hisobga olmasak, u holda Releyning aylanish inersiyasi ta’sirini hisobga olgan tenglamasi kelib chiqadi. Chegaraviy masalalarni yechishda (1.7) va (1.8) aniqlashtirilgan tenglamalar (1.2) va (1.3) munosabatlarga mos holda cheraviy shartlar bilan to’ldiriladi. Bunda chegaraviy shartlar korrektligi haqidagi masala dolzarb hisoblanadi. Ba’zi ishlarda [9, 10, 11] Timoshenkoning tipidagi tenglamalar klassik nazariya chegaraviy shartlari bilan yechiladi, bu esa nokorrekt hisoblanadi. - y o’qi bo’yicha ko’ndalang siljish va x o’qi yo’nalishida bo’ylama siljishning aproksimatsiyalariga asoslangan. (1.10) 10 ; (1.11) Quyida S.P.Timoshenko modeli tavsifini keltiramiz. (1.11) tenglamadagi ikkinchi qo’shiluvchi ko’ndalang kesimlar buzilishini, ya’ni ularning tekislikda siljishini ifodalaydi. (1.10) va (1.11) ifodalarni e’tiborga olib normal va urinma kuchlanishlar uchun qo’yidagi formulalarni hosil qilamiz ; (1.12) ; (1.13) Klassik nazariyadagi ko’ndalang hamda normal kuchlanishlar va (1.12) o’q bo’ylab deformasiyasi bilan bog’lanish ko’ndalang va bo’ylama kuchlanishlarni hisobga olmasdan qabul qilinadi. Eguvchi moment va ko’ndalang kuch uchun integral kattaliklarga o’tib quyidagi ifodalarni olamiz ; (1.14) ; (1.15) (1.14) va (1.15) formulalardagi k- korrektlovchi koeffisiyent, -ko’ndalang kesimda siljishning o’rtacha burchagi, kesim tekisligi buzilishini taxminiy xarakterlovchi -funksiya ko’rinishi shunday olinadiki, kesimda urinma kuchlanishlar taqsimoti materiallar qarshiligi kursidagi kabi, ya’ni ; (1.16) D.I.Jukovskiy formulasiga ko’ra bo’lishi kerak. Shuning uchun (1.12), (1.13) va (1.16) ifodalardan quyidagilarni hosil qilamiz ; (1.17) (1.17) formulalar k korrektlovchi koeffitsiyent kattaligini aniqlashga imkon beradi (masalan, to’g’ri to’rtburchakli ko’ndalang kesim uchun k=615 ) ; (1.18) 11 bog’lanishni kiritib ; (1.19) ifodalarni olamiz, ular (1.7) va (1.8) tenglamalarga olib keladi. (1.3), (1.18) va (1.19) tenglamalarni taqqoslashdan ekanligi kelib chiqadi. (1.10)-(1.19) S.P.Timoshenko modelining tavsifidagi masalaning aniq qo’yilishi matematik approksimasiyasi ma’nosida qat’iy emas. Haqiqatan (1.10) munosabat neytral sirtda aniq bajariladi. (1.19) ifodalar esa faqat egrilik va sterjen siljishi orasidagi bog’lanish hisobga olingan holda o’rinli bo’ladi. S.P.Timoshenko modelini boshqa ko’rinishdagi talqinlari ham bizga ma’lum. Ulardan biri [12] ga tegishli bo’lib, alohida e’tiborga loyiq hisoblanadi. Bir nechta talqinlarning mavjudligi oxir oqibat bir nechta farqli koeffitsiyentlarga ega, bo’lib (1.9) tenglamaga olib keladi. k korrektlovchi koeffitsiyentning mavjudligi S.P.Timoshenko modeliga mos keluvchi gipotezalarni bayon qilishda muhim hisoblanib, keyingi natijalarga olib keladi. S.P.Timoshenko tenglamasi (1.9) to’lqin xarakteriga ega Ya.S.Uflend bu tenglamani yechishda Laplas integral almashtirishlarini qo’lladi va shu bilan bog’liq keyingi tadqiqotlarda qo’llanilgan Riman-Mellin qator integrallarni hisobladi. S.P.Timoshenko bir jinsli bo’magan balka tenglamalarini V.Q.Qabulov, A.Wergandlar qaraganlar. Uzunligi bo’yicha o’zgaruvchi holda va kattaliklar, (1.4) munosabatlarda o’zgarishsiz qoladi u holda (1.7) va (1.8) tenglamalar quyidagi ko’rinishni oladi: (1.20) Agar sterjen bir jinsli elastik muhitda k qattiqlik koeffitsiyenti bilan xarakterlanuvchi ko’ndalang tebranishlar, muhit reaksiyasi -solishtirma bog’lanish sifatida namoyon bo’ladi va (1.9) Timoshenko balka tenglamasiga tegishli hadlar bilan oson to’ldiriladi. Boshlang’ich -ko’chishga va - 12 bo’ylama yuklanishga ega bo’lgan S.P.Timoshenko tipidagi balka tenglamasi E.J.Brunelli ishida keltirilgan. ( ) S.H.Crandall va A.Yildiz, S.P.Timoshenko modeliga asoslanib Foygt bo’yicha tebranishlar ko’ndalang, bo’ylama va yopishqoq elastik so’nishlarda effektlarni hisobga oluvchi differensial tenglamalar sistemasini hosil qilishdilar. (1.21) Bu yerda va so’ndirish koeffitsiyentlari, H. Favre ishida ; (1.22) ; (1.23) munosabatlar bilan ifodalanuvchi qovushoq-elastik materialdan yasalgan sterjen uchun aylanish inersiyasi va siljish deformatsiyasini hisobga olib differensial tenglama olingan. (1.22) bog’lanish Kelvin jisimini da va Maksvell jisimini da tavsiflaydi. Yana va koeffitsiyantlarga nisbatan kichik deb faraz qilinadi, u holda bunday material kvazielastik deb ataladi. Aniqlashtirilgan tenglama ko’rinishga ega. (1.24) 13 Bu yerda -siljishga o’zgarishni hisobga oluvchi keltirilgan yuza. Harakatlanayotgan yoki turg’un uchta to’lqin sinflari qaraladi bular: uzun, o’rta va qisqa to’lqinlar. To’lqinlar uzun deyiladi, qachonki aylanish inersiyasi va siljish e’tiborga olinmasa. O’rtacha to’lqinlarda bu omillar hisobga olinadi, lekin ularning ta’siri kichik deb qaraladi. Qisqa to’lqinlarda aylanish inersiyasi va siljish ta’siri ko’ndalang inersiyasi bilan bir xil tartibda bo’lishi bilan xarakterlanadi. Balandligi h bo’lgan to’g’ri to’rtburchakli sterjen uchun quyidagi hollar olingan: uzun to’lqinlar , o’rta to’lqinlar , qisqa to’lqinlar . Oddiy dempfirlashni hisobga olib ko’ndalang tezlikka va burchak tezlikka proportsional bo’lgan hol J. Gonda tomonidan olingan. (1.25) bu tenglamaning yechimi Laplas almashtirishlariga keltiriladi. Balka aylanish inertsiyasi va siljishini hisobga olingan elastik-plastik dempferlash holidagi buralma tebranishlar tenglamasi M. P. Galin va V.Q.Qabulov ishlarida berilgan. 14 §1.2 Doiraviy elastik silindrik sterjenning buralma tebranishi umumiy tenglamalari Silindrik koordinatalar sistemasida bir jinsli, izotrop va radiusi bo’lgan doiraviy silindrik qovushoq-elastik sterjenni qaraymiz. Tebranish tenglamalarini chiqarishda silindrik sterjenni elastiklik nazariyaga qat’iy bo’ysinuvchi uch o’lchovli jism sifatida deb qaraymiz. Qovushoq-elastik sterjen nuqtalarining ko’chish vektorini quyidagicha keltiramiz , (1. 26 ) bu yerda - bo’ylama va -ko’ndalang to’lqin potensiallari, – z o’qi bo’yicha yo’nalgan birlik vektori [3]. ifodalarini hisobga olib ko’chish vektorini kabi ifodalaymiz. Ko’chish vektorining oxirgi ifodasidagi -birlik vektorlari oldidagi koeffitsientlar mos ravishda - ko’chish komponentalarini aniqlaydi. (1.2 7 ) Deformatsiya va ko’chish orasidagi munosabatlar, 15 ya’ni Koshi munosabatlaridan deformatsiyalarni potensiallar orqali ifodalaymiz (1. 28 ) Bu yerda – hajmiy deformasiya; – uch o’lchamli Laplas operatori. Tebranishlar simmetrik bo’lganida ko’chishlar va deformatsiyalarning (1.27), (1.28) ifodalari quyidagi ko’rinishga keladi , (1. 29 ) va (1.30) Qovushoq-elastik jism uchun Guk qonuniga 16 asosan kuchlanishlar va deformatsiyalar orasidagi quyidagi munosabatga ega bo’lamiz (1.31) -qovushoqlik teskarilanuvchi operatorlari; (1.32) – Lame koeffitsentlari; – qovushoq-elastiklik operatorining ixtiyoriy yadrolari. Silindrik koordinatalar sistemasida sterjen (uch o’lchovli qovushoq-elastik jism) nuqtalarining harakat tenglamalari quyidagicha bo’ladi [5] (1. 33 ) 17 Sterjen nuqtalarining harakat tenglamalariga kuchlanishlarning (1.31) ifodasini va ko’chishlarning (1.27) ifodalarini qo’yib, ba’zi soddalashtirishlardan keyin quyidagiga ega bo’lamiz Bu tenglamalarni mos ravishda - birlik vektorlariga ko’paytirib qo’shamiz, soddalashtirishladan so’ng ushbu tenglikni hosil qilamiz, Bu tenglik o’rinli bo’lishi uchun bo’lishi kerak. Bundan biz quyidagi to’lqin tenglamasiga ega bo’lamiz [2]. (1.34) Bu yerda – sterjen materialining zichligi ; 18 U holda, ya’ni vektori (1.26) kabi tasvirlanganda, -vektor maydonining solinoidallik sharti o’z-o’zidan bajariladi. Endi silindrik qovushoq-elastik sterjenning buralma tebranishlari haqidagi dinamik chegaraviy masalani qo’yamiz. Buning uchun sterjenning buralma tebranishlarini uning sirtida ta’sir etuvchi kuchlanish hosil qiladi deb hisoblaymiz. U holda sterjen uchun chegaraviy shart quyidagicha bo’ladi ; (1.35) Boshlang’ich shartlarni nol deb olamiz. Yuqorida qayd qilingan [1,2] adabiyotlarda ko’rsatilishicha sterjenning buralma tebranishlari faqat potentsial bilan xarakterlanadi. Shuning uchun sterjenning buralma tebranish tenglamasi quyidagi ko’rinishni oladi [1] Sterjenning buralma tebranishlari o’q q a nisbatan simmetrik bo’lganligi uchun buralma tebranishlarni xarakterlovchi barcha parametrlar θ burchakdan bog’liq bo’lmaydi, shu ning uchun potensial ham θ burchakdan bog’liq bo’lmaydi. U holda oxirgi tenglama quyidagi ko’rinishni oladi. (1.36) Shunday qilib buralma tebranishlarda sterjen nuqtalarining harakati (1.36) tenglama orqali ifodalanadi. Chegaraviy shartlar (1.35) va boshlang’ich shartlar nol deb olinadi. Masalani yechish uchun potentsialni ushbu ko’rinishda tasvirlaymiz [4] (1.37) bu yerda l - p tekislikning uchastkasidan o’ngda joylashgan ochiq kontur, potensialning bu ifodasinidan va larni topamiz, 19 hosil qilingan ifodalarni (1.36) harakat tenglamasiga qo’yib, soddalashtirishlardan keyin quyidagiga ega bo’lamiz , bunda kabi belgilashlar olsak quyidagini hosil qilamiz. , (1.38) Yuqoridagi (1.38) tenglamaning umumiy yechimi , (1.39) ga teng, bunda I 0 – modifikasiyalangan Bessel funksiyasi [6]. Modifikasiyalangan Bessel funksiyasi uchun quyida qo’llaniladigan ba’zi munosabatlarni keltiramiz [5] (1.40) Sterjen sirtida ta’sir etuvchi kuchlanish ifodasini ham (1.41) kabi tasvirlab (1.37) ifodani hisobga olsak (1.35) chegaraviy shart quyidagi ko’rinishni oladi ; (1.42) bunda . Agar (1.39) umumiy yechimini va (1.40) munosabatlarni hisobga olsak, (1.42) chegaraviy shart quyidagicha bo’ladi 20 (1.43) endi ko’chishni ham (1.44) kabi tasvirlaymiz. potensial va ko’chish ifodasini (1.29) formuladagi ikkinchi tenglikka qo’yamiz Oxirgi tenglikka (1.39) umumiy yechimni qo’yib (1.45) ifodaga ega bo’lamiz. Ko’chishning ushbu ifodasidagi Besselning -modifikasiyalangan funksiyasini r radial koordinata bo’yicha qatorga yoyamiz. U holda quyidagiga ega bo’lamiz (1. 46 ) Oxirgi (1. 46 ) tenglamada n=0 va deb hamda (1.47) kabi almashtirish olib quyidagini hosil qilamiz (1.48) Keltirilgan (1.48) ifodadan ko’rinadiki almashtirilgan funksiya deformatsiya o’lchov birligiga ega. Bu (1.48) formula masalaning aniq matematik qo’yilishi va uning aniq yechimidan kelib chiqadi. Integrallash o’zgarmasi ni (1.47) tenglikdan topib (1.46) formulaga qo’yamiz. Natijada ko’chishning almashtirilgan funksiya orqali ifodasini hosil qilamiz (1.49) 21 Chegaraviy shartning (1.43) ifodasidagi I 2 funksiyani bo’yicha qatorga yoyib, hamda integrallash o’zgarmasi o’rniga uning (1.47) ifodasini qo’yib quyidagini hosil qilamiz (1.50) Endi funksiya va operatorlarni quyidagi ko’rinishda kiritamiz (1. 51 ) U holda (1. 50 ) tenglama ushbu ko’rinishda bo’ladi (1.52) bu yerda (1.53) Yuqorida kabi belgilangan ifodaga asosan (z,t) o’zgaruvchili operatorning quyidagiga tengligini ko’rish qiyin emas [4] (1.54) Hosil qilingan (1.52) ifoda (1.54) ga muvofiq operator uchun sterjen ko’chishining bosh qismiga nisbatan tartibi cheksiz katta bo’lgan integro-differensial operatorni o’z ichiga oladi. Shunday qilib doiraviy sterjen nuqtalari buralma tebranishining bosh ko’chishlariga nisbatan umumiy tenglamalari (1.52) tenglama hisoblanadi. Bu tenglama t vaqt va z koordinata bo’yicha ixtiyoriy tartibli hosilani o’z ichiga oladi. Ko’chishning (1.49) ifodasidan quyidagini topamiz (1.55) bunda (1.56) Sterjenning ixtiyoriy nuqtasidagi ko’chishni, (1.52) tenglama yechimi natijalari va (1.55), (1.56) formulalar orqali olish mumkin. 22 Sterjenning buralma tebranishlarida faqat ko’chish va va kuchlanishlar noldan farqli bo’ladi. Ularni funksiya orqali ifodalaymiz. Buning uchun , kuchlanishlarni (1.57) kabi tasvirlab, ularnng bu ifodalarini va -potensialning (1.37) ko’rinishini (1.31) formulaning va ifodasiga qo’yamiz Hosil qilingan bu ifodaga (1.39) yechimidan (1.40) munosabatlarni hisobga olib tegishli hosilalar olsak, qo’yidagi ifodalarga ega bo’lamiz (1.58) Hosil qilingan (1.58) ifodadagi I 1 va I 2 - modifikatsiyalangan Bessel funksiyasini radial koordinata bo’yicha qatorga yoyib va o’zgarmasning qiymatini (1.47) formula bo’yicha qo’yamiz va kuchlanishlar uchun (1.59) ifodaga ega bo’lamiz. Yuqoridagi va belgilashlarni hisobga olib (1.59) ifodani quyidagicha yozamiz (1.60) bu yerda –operatorlarni mos ravishda (1.56) va (1.53) formulalar orqali aniqlaymiz. 23 Olingan (1.52) tenglamalar doiraviy silindrik qovushoq-elastik sterjen buralma tebranishlari uchun umumiy hisoblanadi. Kuchlanishlarning (1.60) va ko’chishlarning (1.55) formulalari yordamida sterjenning ixtiyoriy kesimida vaqtning ixtiyoriy momentidagi kuchlanganlik-deformatsiyalanganlik holatini hohlagan aniqlikda topish mumkin. §1.3. Doiraviy elastik silindrik qobiqning buralma tebranishlarida deformarsiyalanuvchi muhit ta’sirini e’tiborga olish Silindrik qobiq va qatlamlar buralma tebranishlari haqidagi masalani urganishda doiraviy silindrik qatlamning buralma tebranish tenglamalaridan foydalanamiz. Ushbu nazariya slindrik qatlamlar uchun ham o'rinli ekanligi [8] ishlarida keltirilgan. Unga ko’ra anizotrop slindrik qatlamning buralma tebranishlarida buralma kuchishlarni e’tiborga olib asosiy tenglamalar sistemasini quyidagicha yozishimiz mumkin ( 1.61) 24 bu yerda - integrodifferensial operator; (1.62 ) b 0 – ko`ndalang to`lqin tarqalish tezligi ; - siljish moduli; - izotropiya tekisligiga perpendikulyar tekislikning ciljish moduli; Bu erda formulalar otqali ifodalanadi. Bu yerda - Puasson koeffitsientlari, E, E ’ - elastiklik modulari. - qatlam nuqtalari buralma kuchishlari bosh qismlari; (1.63) va - qatlam ichki va tashqi radiuslari; - qatlam o`rta sirtining radiusi bo’lib u quyidagi formula bilan topiladi: - deformatsiyalanuvchi muhit reaksiyasi bo'lib doiraviy slindrik qobiq va qatlamlar uchun quyidagicha qabul qilinadi. 25 va - qovushoq elastik operatorlar bo’lib qobiq materiali holatiga bog'liq. Qobiq uchun "nol" o'rab turuvchi muhit uchun "1" bo’lishi mumkin: - Lame koeffitsentlari qobiq materiali uchun (m=0), muhit uchun (m=1); - qovushoq elastik operator. Bunda va (m=0,1) - teskari operator deb faraz qilinadi. - bu ham operator hisoblanib, o'rab turuvchi muhit ta'sirini hisobga oladi. Kuchish va kuchlanishlar formulalarini quyidagi kuchishlar orqali yozish mumkin: (1.64) 26 (1.64’) bu yerda - integridifferensial operator. O’rab turuvchi muhit ta’sirini hisobga olgan holda ko’chishlarga nisbatan aniqlashtirilgan tebranish tenglamalarini quyidagicha yozamiz (1.65) Bu yerda qatlam ko’chishlarining bosh qismlari; - tashqi kuch funksiyalari; -chiziqli differensial operator; o’rab turuvchi muhit reaksiyasi; 27hr  1r 2r z  b) h r  1r 2r a) 1 2 r r h   Dissertatsiya doirasida kuchlanishlarga nisbatan chiqarilgan (1.65) tenglamalar sistemasini masalalar yechishda qullaymiz. Quyida uzunligi chekli bo’lgan chetlari sharnirli tayangan doiraviy elastik slindrik qatlamning buralma tebranishlariga aylanish inersiyasi va ko'ndalang siljish deformatsiyasi ta'sirini qarab chiqamiz. Asosiy tebranish tenglamalari sifatida aniqlashtirilgan [2] tebranish tenglamalari (1.65) dan foydalanamiz, bunda qobiq materialini elastik, qobiq sirtida tashqi ta'sirlar va tashqi muhit ta'siri yo'q deb (1.65) tenglamalar sistemasini quyidagi kurinishga keltiramiz (1.66) 281-Rasm. Silindrik qobiq bu yerda lar kuchishlarining bosh qismlari bo’lib u quyidagiga teng : (1.66) da tashqi kuchlar ta’sirini va o’rab turuvchi muhit ta’sirini hisobga olmasak operatorning chiziqliligidan foydalansak (1.67) bo’ladi. U holda ba’zi bir matematik almashtirishlardan song quyidagi ikkita tenglamaga ega bo’lamiz (1.68) (1.69) Bu yerda -Puasson koeffitsienti, - Lame koeffitsientlari, - qatlam materiali zichligi, -qatlam oraliq sirti radiusi. Ushbu (1.68) tenglamada -ni hisobga olsak qatlam tebranishlari klassik holga mos keladi (sterjenlar nazariyasiga ko’ra). Shuning uchun keyingi hisoblarimizda 29 (1.68) tenglamalar sistemasidagi ikkinchi tenglamadan foydalanamiz. Hosil qilingan tenglamani ga ko'paytiramiz, bu yerda - qatlam ko’ndalang kesimi inersiya momenti; -operatorni teskari kurinishda yozsak (1.69) ni ba'zi bir almashtirishlardan keyin quyidagicha yozamiz , (1.70) bu yerda E - qatlam materiali elastiklik moduli; F - qatlam kundalang kesimi yuzasi; (1.70) tenglamalarda va koefitsientlar ko’ndalang siljish deformatsiyasi ta’sirini hisobga oladi, - aylanish inersiyasi ta'sirini; - 30 bo'ylama kuch inersiyasi ta'sirini; - reaktiv moment, - bo'ylama tekis taqsimlangan kuchni hisobga oladi. Ushbu (1.70) tenglamaga va parametrlarini kiritamiz. Bu parametrlar “nol” va “bir” qiymatlarni qabul qiladi . Y a'ni aylanish inersiyasi va ko’ndalang siljish deformatsiyasi ta’siri bor yoki yo'q ekanligini bildiradi. (1.70) tenglamada ulchamsiz koordinataga utamiz, ya'ni bu yerda va yozish osonlashish uchun keyingi yozuvlarda yo'duzchalarni tashlab ketamiz . (1.71) K eyingi boblarda u shbu keltirib chiqarilgan (1.71) tenglamadan amaliy masalalar yechishda foydalanamiz . §1.4 Doiraviy elastik silindrik sterjenning buralma tebranishlari asosiy tenglamalari (xususiy hol) Yo’qoridagi paragrafda keltirib chiqarilgan (1.52) tenglama doiraviy elastik sterjenning buralma tebranishi uchun umumiy tenglama hisoblanadi. Bu tenglama ko’chishlarning bosh qismlariga nisbatan keltirilib chiqarildi. Sterjenning sirti unga ta’sir etuvchi kuchlanishlardan holi deb hisoblab, sterjen buralma tebranishining klassik va aniqlashtirilgan tenglamalarini keltirib chiqaramiz. 31 Avvalo elastik sterjenning umumiy (1.52) tenglamasidan elastik sterjen uchun klassik buralma tebranish tenglamasiga yaqin, lekin undan umumiy bo’lgan tenglamani chiqaramiz. Buning uchun (1.53) formulada deb va (1.54) munosabatni hisobga olib quyidagiga ega bo’lamiz Hosil qilingangan ning ifodasini (1.52) tenglamaga qo’yib ushbuni olamiz Oxirgi tenglikni har ikkala tomonini ga bo’lib (1.72) qovushoq-elastik sterjen buralma tebranishlarining tenglamasiga ega bo’lamiz. Bu tenglamaning tartibi ikkiga teng. Undan bo’lgan hol uchun ushbu elastik sterjenning buralma tebranishlari tenglamasi kelib chiqadi. (1.73) Hosil qilingan (1.71) tenglamada ekanligini hisobga olsak, bu tenglama elastik sterjenning buralma tebranish klassik tenglamasidan iborat ekanligi ko’rinadi. Shunga mos ravishda (1.61) tenglamani ham elastik sterjenning buralma tebranish klassik tenglamasi deb ataymiz. Sterjenning buralma tebranishlari aniqlashtirilgan tenglamasini keltirib chiqarish uchun (1.53) ifodada deb qaraymiz va quyidagi tenglikni hosil qilamiz (1.54) munosabatni e’tiborga olgan holda ifodani (1.52) tenglamaga qo’yib quyidagiga ega bo’lamiz 32 Bu tenglikni har ikkala tomonini ga bo’lib, ikkinchi qavsni kvadratga ko’taramiz va quyidagini olamiz (1.74) Hosil qilingan bu tenglama qovushoq-elastik sterjen buralma tebranishlari aniqlashtirilgan tenglamasi hisoblanadi. Bu tenglama to’rtinchi tartibli bo’lib undan bo’lgan hol uchun elastik sterjenning buralma tebranishlari aniqlashtirilgan tenglamasini hosil qilamiz. (1.75) Ushbu (1.75) tenglamada ekanligini hisobga olsak elastik sterjenning buralma tebranish aniqlashtirilgan tenglamasiga ega bo’lamiz. Shunga mos ravishda (1.74) tenglamani ham qovushoq-elastik sterjenning buralma tebranishi aniqlashtirilgan tenglamasi deb ataymiz. Hosil qilingan (1.74) tenglamani ko’ndalang kesim yuzasi doiraviy bo’lgan sterjenning markaziy o’qiga nisbatan inertsiya momenti va qovushoqlik teskarilanuvchi operatori ga ko’paytirib quyidagi tenglamaga kelamiz. Bu yerda ko’ndalang kesimi doiraviy bo’lgan sterjenning markaziy o’qiga nisbatan inersiya momenti va sterjenning ko’ndalang kesim yuzasi ekanligini hisobga olsak yo’qoridagi tenglamani (1.76) ko’rinishida yozish mumkin bo’ladi. 33 Bu tenglamada deb va ekanligidan ga ega bo’lamiz. Agar ( - Puasson koeffitsienti, ) kabi belgilash olsak, oxirgi tenglamani quyidagicha yozish mumkin (1.77) Keltirib chiqarilgan (1.77) tenglamadagi hadlarning mexanik ma’nosi haqida to’xtalib o’tamiz: -aylanish inersiyasining ta’siri; -tekis taqsimlangan kuch; -inersiya kuchlari; -ichki kuchlanish kuchlari. Oxirgi (1.77) tenglamadan faqat aylanish inersiyasi hisobga olinsa, (1.78) tenglamaga, faqat ko’ndalang siljish deformatsiyasi hisobga olinsa, (1.79) tenglamaga, faqat taqsimlangan kuchlar hisobga olinsa (1.80) tenglamaga ega bo’lamiz. 34 II-BOB. DIFFERENSIAL TENGLAMALARNI YECHISHNING SONLI USULLARI §2.1 С hekli ayirmalar usulini d ifferentsial tenglamalar yechishda qo’llanilishi Plastinkalar va qobiqlar nazariyasining qator masalalari berilgan chegaraviy shartli xususiy xosilali deferensial tenglamalarga keltiriladi. Bu tenglamalar oddiy masalalar hamda chegaralar va tashqi yuklarning oddiy shakllaridagina aniq yechiladilar. Ko’p hollarda aniq yechimlarni topish qiyin bo’ladi. Shuning uchun sonli usullarga murojaat qilinadi. Xususan shunday sonli usullardan biri differensial tenglamalarni tegishli chekli ayirmalar qatnashgan tenglamalar bilan almashtirishdan iboratdir. Chekli ayirmalar metodining imkoniyati EHM paydo bo’lishi bilan oshib ketdi. Plastinkalar va qobiqlar nazariyasi masalalarini chekli ayirmalar usuli yordamida yechishga doir ilmiy ishlar keskin ko’paydi. Biz quyida [9] ishdan foydalangan holda chekli ayirmalar usulining asosiy mohiyatini bayon qilamiz. Xususiy xosilali differensial tenglamalarni taqribiy yechishda to’rlar yoki chekli ayirmalar metodining asosiy g’oyasi quyidagilardan iborat:  yechim qidirilayotgan G soha to’rli soha bilan almashtiriladi; – berilgan differensial tenglama sohaning ichki nuqtalarida tegishli chekli ayirmalar qatnashgan tenglamalar bilan almashtiriladi; – chegaraviy shartlar asosida qidirilayotgan yechimning qiymatlari soha tugunlarida topiladi. Bunday almashtirish natijasida ko’p noma’lumli algebraik tenglamalar sistemasiga kelamiz. Bunda noma’lumlar soni tenglamalr soni va tugunlar soni ko’paytmasiga teng bo’ladi. Bu sistemani yechib izlanayotgan funksiyaning nuqtalardagi sonli qiymatlarini hosil qilamiz. Funksiyaning boshqa nuqtalaridagi qiymatlari interpolyasion formulalardan topiladi. 35 To’rli sohani tanlash har bir aniq masalaga qarab amalga oshiriladi, biroq hamma vaqt kontur G ni yaxshiroq approksimatsiya qilishga intiladi. To’rli soha kvadrat, to’g’ri to’rtburchak, uchburchak, oltiburchak va boshqa elementlardan iborat bo’lishi mumkin. R n qoldiq hadning qiymatlari alohida elementning o’lchamlaridan bog’liq bo’ladi. Ya’ni o’lchamlar qancha kichik olinsa R n qoldiq had shuncha kichik bo’ladi. Ammo tugunlar soni ortib ketishi natijasida tenglamalar soni ko’payadi va uni EHM da yechish amalda mumkin bo’lmay qoladi. Ma’lumki funksiuaning nuqtadagi hosilasi quyidagicha topiladi: Bu yerda - argumentning chekli orttirmasi, bo’lganda birinchi formulaga o’ng hosila, ikkinchi formulaga esa chap hosila deyiladi. Yuqorida berilgan formulada limit simvolini tushurib qoldirsak o’ng va chap hosilalar uchun ushbu taqribiy formulalarni olamiz. (2.1) Amalda nuqtada markaziy ayirmalardan ham foydalanadi (2.2) Ikkinchi tartibli chekli ayirma xosila uchun (2.3) formuladan foydalanish qulay. Yuqoridagi (2.2) va (2.3) ifodalar asosida yuqori tartibli chekli ayirmali xosilalar uchun formulani keltirish mumkin Hosilalarning almashtirishning bu usuli uning aniqligini baholashga imkon bermaydi. 36 Funksiya hosilalarining uning diskret nuqtalaridagi qiymatlari orqali almashtirib approksimatsiya xatosining bahosini ham beruvchi turli usullar mavjud. Quyida Teylor formulalariga asoslanuvchi usuldan foydalanamiz. O’ng chekli ayirmali hosila Teng uzoqlikda joylashgan nuqtalar uchun qiymatlari ma’lum bo’lsin, bunda - o’qi bo’yicha qadam (1- rasm). (2.4) kattalikka funksiyaning nuqtadagi o’ng ayirmasi deyiladi. Ikkinchi o’ng ayirma esa birinchi ayirmadan olingan ayirma hisoblanadi. Xuddi shu yo’l bilan yuqori tartibli ayirmalarni ham topish mumkin. Shunday qilib nuqtada -tartibli o’ng ayirmani topish uchun ushbu formuladan foydalanamiz. (2.5) Endi nuqtada ayirmali operator va differensial operatorlar orasidagi bog’lanishni aniqlaymiz. Buning uchun va funksiyalar Teylor qatoriga yoyiladi (2.6) Ushbu belgilashlarni olamiz u holda 372 i 1 i i 1 i 2 i   x 2.1-rasm Hosil qilingan bu ifodaga (2.6) formulani ikkinchisini qo’llab quyidagicha yozish mumkin (2.7) (2.7) ni (2.4) ga qo’yib quyidagini olamiz ; Bu yerdan , operatorlar orasidagi quyidagi bog’lanishga ega bo’lamiz. yoki ; (2.8) (2.9) ni n-darajaga ko’tarib n-tartibli hosila operatori orasida bog’lanishni topamiz ; (2.9) (2.9), (2.10) formulalarni amalda tadbiq etish uchun ni bo’yicha qatorga yoyamiz. (2.10) Shunday qilib (2.11) Bu formula yordamida funksiyaning nuqtadagi xosilasi ixtiyoriy aniqlikda o’ng ayirmalar orqali ifodalash mumkin. Chap ayirmali hosilalar funksiyaning nuqtadagi birinchi chap ayirmasi yoki chap ayirmasi deb ushbuga aytamiz. (2.12) Bu yerda chap ayirma o’ng ayirmadan farqli ravishda (nabla) bilan belgilandi, yuqori tartibli ayirmalar (2.13) Yuqoridagi (2.6) yoyilmani lar uchun ishlatsak: 38 (2.14) hosil qilingan (2.14) ni (2.12) ga qo’ysak U holda va operatorlari orasida bog’lanish topiladi: yoki (2.15) ni ning darajalari bo’yicha qatorga yoyib, hosila operatorini chap ayirmalar operatori orqali ifodalaymiz: (2.16) n-tartibli chap ayirmali hosilalarni chap ayirmalar orqali (2.15) ni m - darajaga ko’tartish yo’li bilan hosil qilamiz: (2.17) Bu yerda ayirma tartibga ega ekanligini ko’ramiz. operatorlar orasida ushbu bog’lanish mavjud (2.18) Markaziy ayirmali hosilalar funksiyaning nuqtadagi birinchi markaziy ayirmasi yoki markaziy ayirmasi deb ushbu ifodagi aytiladi (2.19) Yuqoridagi kabi yuqori tartibli ayirmalarni ham kiritish mumkin. Masalan, , (2.20) 392 i 1 i i 1 i 2 i   x 2.2-rasm  2/1 i 2/1 i Barcha toq tartibli markaziy ayirmalar funksiyaning nuqtalardagi qiymatlari orqali, barcha juft tartibli markaziy ayirmalar esa funksiyaning nuqtalaridagi qiymatlari orqali hisoblanadi. Bunday yozuvdan qutulish uchun o’rtalashgan markaziy ayirma tushunchasi kiritiladi. O’rtalashtirish operatorini quyidagicha kiritamiz (2.21 ) Buning yordamida birinchi tartibli o’rtalashgan ayirma quyidagicha yoziladi ; (2.22 ) O’rtalashgan uchinchi ayirma (1.21 ) va (1.22 ) ga asosan . (2.23 ) Barcha toq o’rtalashgan ayirmalar ayirma yuqoridagi kabi topiladi. operatorlarni o’zaro bog’lash mumkin bundan (2.24) Ikkinchi tomondan funksiyani va nuqtalarda Teylor qatoriga yoyib ushbuni olamiz: (2.25) 40 Birinchi tartibli hosila operatori o’rtallashgan markaziy ayirma orqali quyidagicha ifodalanadi (2.26) bunda ushbu yoyilmadan foydalanamiz (2.25) tenglikni hisobga olsak bu ifodani ko’rinishi quyidagicha bo’ladi Bu ifodani ni darajasini o’sib borish tartibida yozamiz (2.27) Oxirgi yoyilmadan foydalanib ixtiyoriy tartibli markaziy ayirmani topish mumkin. (2.27) dan ko’rinadiki yoyilmaning bitta hadining qo’shilishi approksimatsiya aniqligini ga oshiradi. Bundan tashqari markaziy ayirmali hosilalar bir tomonli hosilalarga nisbatan aniqlik darajasi katta . Yuqori tartibli hosilalarni (2.27) dan uning o’ng va chap tomonlarini - darajaga ko’tarish yo’li bilan hosil qilamiz, bunda juft darajalarda (2.24) ni hisobga olamiz. (2.28) Oxirgi formulada bo’lganda ; ; ; Keltirib chiqarilgan (2.28) formuladan ixtiyoriy tartibli markaziy ayirmali hosilani aniqlashimiz mumkin. 41 § 2.2. Differentsial tenglamalarni taqribiy yechish Xususiy hosilali differentsial tenglamalar. Ikki noma’lumli o‘zgaruvchiga bog‘liq bo‘lgan u=u(x,y) funktsiyaning ikkinchi tartibli xususiy hosilali differentsial tenglamasini quyidagi ko‘rinishda yozamiz. (2.29) Bu yerda , u erkli o‘zgaruvchilar, u izlanayotgan noma’lum funktsiya, lar esa x,u erkli o‘zgaruvchilar bo‘yicha bir va ikkinchi tartibli xususiy hosilalar hisoblanadi. (2.29) tenglamaning yechimi deb, uni ayniyatga aylantiruvchi u=u(x,u) funktsiyaga aytiladi. Bu ye chim grafigi Oxuu fazoda sirtni ifodalaydi. 42 Agar (3.29) tenglamada u izlanayotgan noma’lum funktsiya va uning xususiy hosilalari ning darajalari birinchi bo‘lsa hamda ularning ko‘paytmalari ishtrok etmasa bunday tenglamani chiziqli deb ataladi. Uni quyidagicha yozish mumkin: (2.30) Bu yerda A,B,S , a,b,s koeffitsentlar o‘zgarmas yoki x,u erkli o‘zgaruvchilarning funktsiyalari bo‘lishi mumkin. (**) o‘zgarmas koeffitsentli tenglama bo‘lsin. (2.30) tenglama diskriminanti D=AC-B 2 ni tuzamiz , buning ishorasiga qarab tenglama turini aniqlaymiz: agar D>0 ( 2.30 ) elliptik turdagi tenglama ; agar D=0 ( 2.30 ) parabolik turdagi tenglama ; agar D<0 ( 2.30 ) giperbolik turdagi tenglama . 1 . Agar ( 2.30 ) da A=1, B =0, S=1 bo‘lsa, elliptik turdagi Laplas tenglamasi deyiladi. Bu tenglama u=u(x,y) issi qlikni ‘lastinkaning (x,y) nuqtasda vaqtga bog‘liq bo‘lmagan holda tarqalishini ifodalaydi. 2. Agar (**) da A = - a 2 , a=1, B=0,C=0, b=0, c=0 bo‘lsa, bu parabolik turdagi tenglama bo‘lib, u t vaqt birligi ichida x koordinata bilan ingichka bir jinsli sterjen bo‘yicha u=u(x,t) issiqlikni tarqalishini ifodalaydi. F(x,t) –issiqlikni jisim bo‘yicha manbadan tarqalish zichligi bilan bog‘liq funktsiya, agar bu funktsiya ishtrok etmasa bu tenglama birjinsli bo‘ladi. . a- sterjenning fizik xossasiga bog‘liq bo‘lgan o‘zgarmas. C h ekli ayirmalar usuli yoki to‘r usuli Chekli ayirmalar usuli xususiy hosilali tenglamalarning sonli yechimini topishda eng qulay usullardan biridir . Bu usulining asosida hosilarni chekli ayirmalar nisbati bilan almashtirish qoidasi yotadi . 43 Aytaylik, Oxy koordinatalar tekisligida chegarasi T chiziq bilan chegaralangan yo‘ik G soha berilgan bulsin. G sohani kesib o‘tuvchi o‘qlarga parallel bo‘lgan to‘g‘ri chiziqlar oylasini quramiz : Bu to‘g‘ri chiziqlarning kesishish nuqtalarni tugunlar deb ataladi. Hosil bo‘lgan turda ikki tugunni qo‘shni tugun deb ataladi. Agar ular biri ikinchisidan OX yoki OU koordinata o‘qlari yunalishida h yoki l masofada joylashgan bo‘lsa G+Г sohaga tegishli bo‘lgan va sohaning chegarasi G dan, qadamdan kichik masofada turgan tugunlarni ajratamiz. Sohaning biror tuguni va unga qo‘shni bo‘lgan turtta tugun ajratilgan tugunlariga tegishli bo‘lsa, bu tugunni ichki tugun deb ataladi. (2-rasm, A tugun). Ajratilganndan qolganlari chegara tugunlari deb ataladi(2-rasm, B, C tugunlar). Noma’lum funktsiyaning t o‘ rning 5 yoki 9 tugunli sxemalarining tugunlaridagi qiymatini orkali belgilaymiz. Har bir ichki nuqtadagi xususiy hosilalarni ayirmalar nisbati bilan quyidagicha almashtiramiz: 44 ( 2.31 ) CHegaraviy nuqtalarda esa aniqligi kamroq bo‘lgan quyidagi formular bilan almashtiramiz: (2.32) Xuddi shuningdek, ikkinchi tartibli xususiy hosilarni quyidagicha almasht’ramiz: (2.33) Yuqorida ketirilgan almatiririshlar xususiy hosilasi tenglamalarni o‘rniga chekli ayrimali sistemasini yechishga olib keladi. Yuqorida ko‘rsatilgan sohada quyidagi masalani ko‘ramiz. ( 2.34 ) bu yerda a,c,d,e,g lar x va y larning funktsiyalari. (x i ,y k ) tugunda f(x,y) funksiya va koeffitsentlarni a ij , b ij , c ij , d ij , g ij , f ij, u ij kabi belngilab, besh nuqtali tugunlar sxemasi bo‘yicha (2.31), (2.32) formulalar asosida chekli ayirmalar yordamida (2.31) tenglamani quyidagicha yozamiz. a ik + b ik + c ik + + d ik - g ik u ik = f ik ( 2.35 ) 45 S h uningdek G chegara chiziq funksiyasi asosida chegara tugunlari yoki (0 < <1 )uchun quyidagi munosabatlarni yozamiz: yoki . Agar tenglama tarkibida ishtrok etsa uni to‘qqiz nuqtali tugunlar sxemasi bo‘yicha chekli ayirmalar bilan quyidagicha almashtirib (2.35) tenglamaga qo‘shamiz. = Chekli ayirmalar yordamida (2.34) tenglamani, (x i ,y k ) tugunga nisbatan hosilbo‘ladigan tenglamalar sistemasini quyidagicha yozamiz: A i,k u i,k +B i,k u i,k-1 +C i,k u i,k +D i,k u i+1,k +E i,k u i,k+1 = f i,k ( 2.36 ) , , , , Farazimizga asosan a(x,u) > 0 , b (x,u) < 0 , g (x,u) < 0 lar silliq funktsiyalar bo‘lsa, etarlicha kichik h uchun g i,k <0, A i,k >0, B i,k >0, C i,k <0, D i,k >0, E i,k >0 bo‘lganda quyidagi tenglikka ega bo‘lamiz: A i,k +B i,k +C i,k +D i,k +E i,k = g i,k. 46 Hosil bo‘lgan chiziqli tenglamalar sistema (2.36) si uchun yuqoridagi shartlar bajarilganda bu sohaning ichki tugunlarida sistemani yechimini topishda iteratsiya usulini qullash uchun uni quyidagi ko‘rinishga keltiramiz. SHuningdek chegaraviy tugunlar uchun Berilgan boshlang‘ich echim asosida aniq yechimga yaqinlashish jarayonini oddiy iteratsiya usulida quyidagicha hisoblaymiz: , i =0,1,2,… Yuqoridagi shartlar asosida bu jarayonni u i,k aniq yechimga yaqinlashish sharti quyidagicha tanlanadi: 47 48 III-BOB DOIRAVIY ELASTIK SILINDRIK QOBIQNING BURALMA TEBRANISHLARI §3.1. Doiraviy elastik silindrik qobiqning buralma tebranish tenglamalarida aylanish inersiyasi ta’siri Maskur magistrlik dissertasiyasi doirasida mateiali transversal-izotrop doiraviy silindrik qatlamning buralma tebranishlariga aylanish inersiyasi ta`sirini ikkinchi bobda keltirilgan sonli usullar yordamida qarab chiqamiz. Silindrik qobiq va qatlamlar buralma tebranishlari haqidagi masalani tadqiq qilishda doiraviy silindrik qatlamning buralma tebranishlari tenglamalaridan foydalanamiz. Ushbu nazariyani silindrik qatlamlar uchun ham o'rinli ekanligini [8] ishlarida keltirib o’tilgan. Dissertatsiya ishining uchinchi bobi “Doiraviy elastik silindrik qobiqning buralma tebranishlari” deb nomlangan. Bob ikkita paragrafdan iborat bo’lib birinchi paragrafda qobiq ichki va tashqi radiuslarini hisobga olgan holda aylanish inersiyasi hisobga olingan hollar uchun yechilgan. Olingan sonli natijalar asosida, ko’chishlarning vaqtdan va koordinataga bog’liq grafiklari keltirilgan. 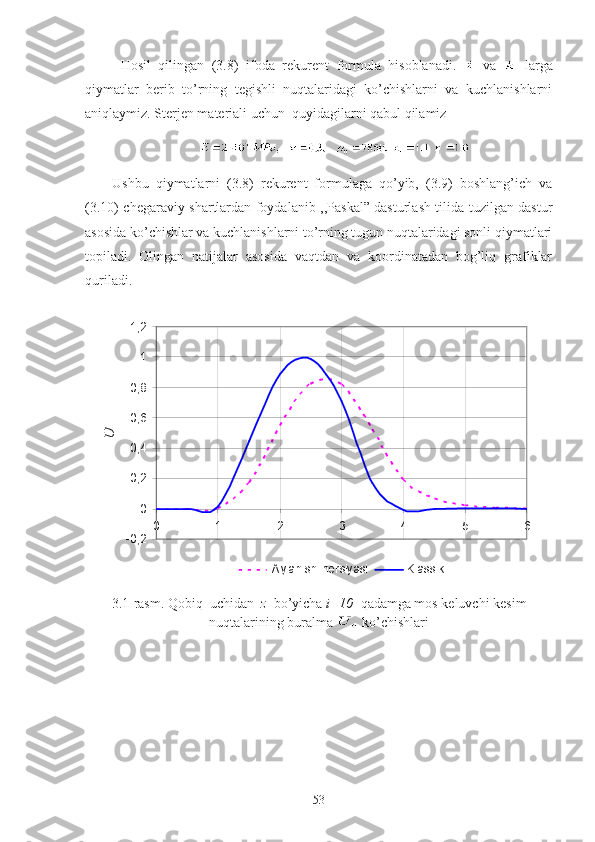Uzunligi ga teng, chetlari sharnirli tayangan, ko’ndalang kesimi doiraviy bo’lgan silindrik elastik qobiq uchun vaqtning ixtiyoriy momentidagi kuchlanganlik va deformatsiyalanganlik holatini, berilgan boshlang’ich va chegaraviy shartlar asosida sohada, aylanish inersiyasi ta’sirini hisobga 49 olgan holda aniqlash talab etilgan bo’lsin. Qobiqning sirtida kuchlanishlar yo’q deb qaraymiz. Masalani yechishda aylanish inersiyasi ta’sirini hisobga olganda buralma tebranishlarining (1.75) differensial tenglamasidan foydalanamiz. . bu yerda E - qatlam materiali elastiklik moduli; -Puasson koeffitsienti. Quyidagicha almashtirish olamiz: u holda (3.1) tenglama quyidagi ko’rinishga keladi; (3.2) O’rganilayotgan sohani -to’g’ri to’rtburchakli to’r bilan koordinata bo’yicha , vaqt bo’yicha qadamlar bilan ajratib olamiz 50 -yechimning aniqligini ta’minlovchi koeffitsiyentlar. Masala shartiga ko’ra boshlang’ich va chegaraviy shartlarini aniqlaymiz. Faraz qilaylik, kinematik qo’zg’atish funksiyasi dan iborat bo’lsin. Bu yerda A -amplitudani ifodalovchi o’zgarmas, 1t - vaqtning fiksirlangan momenti. Sterjen erkin uchida , qistirib mahkamlangan uchida esa bo’lganligi uchun chegaraviy shartlarni yozamiz: (3.3) boshlang’ich shartlar: ; (3.4) dan iborat bo’ladi. Tenglamadagi -hadlarni chekli ayirmalar orqali yozib olamiz: -izlanayotgan funksiyaning to’r tugunidagi qiymati. 51 Bu ifodalarni hisobga olib, (3.2) doiraviy elastik qobiqning buralma tebranishlari tenglamasini chekli ayirmalar orqali tasvirlaymiz = + + + (3.5) Hosil qilingan (3.5) da va larni quyidagicha yozamiz: (3.6) (3.7) Ushbu tenglamalar sistemasini yechishda -larga nisbatan gruhlab chiqib, ba’zi bir matematik almashtirishlardan so’ng (3.6) ni quyidagicha yozamiz (3.8) boshlang’ich shartlar: da , ; (3.9) chegaraviy shartlar: da , da . (3.10) Yuqorida keltirilgan (3.8), (3.9), (3.10) lar birgalikda chegaraviy masalani tashkil qiladi. 52 Hosil qilingan (3.8) ifoda rekurent formula hisoblanadi. va larga qiymatlar berib to’rning tegishli nuqtalaridagi ko’chishlarni va kuchlanishlarni aniqlaymiz. Sterjen materiali uchun quyidagilarni qabul qilamiz Ushbu qiymatlarni (3.8) rekurent formulaga qo’yib, (3.9) boshlang’ich va (3.10) chegaraviy shartlardan foydalanib ,,Paskal” dasturlash tilida tuzilgan dastur asosida ko’chishlar va kuchlanishlarni to’rning tugun nuqtalaridagi sonli qiymatlari topiladi. Olingan natijalar asosida vaqtdan va koordinatadan bog’liq grafiklar quriladi. -0,2 00,20,40,60,8 11,2 0 1 2 3 4 5 6 tU Aylanish inersiyasi Klassik 3.1-rasm. Qobiq uchidan z bo’yicha i=10 qadamga mos keluvchi kesim nuqtalarining buralma ko’chishlari 53 3.2- rasm . Qobiq uchidan z bo ’ yicha i =50 qadamga mos keluvchi kesim nuqtalarining buralma ko ’ chishlari . Olingan natijalarni grafik ko’rinishida tasvirlaymiz. 3.3-rasm 54i =25 Klassik i =50 Klassik tU 3.4-rasm Olingan natijalar 3.3, 3.4-rasmlarda buralma ko’chish va vaqtdan bog’liq grafiklar tasvirlangan. 3.3-rasmda i=25 va i=50 (z bo’yicha) qadamga mos keluvchi kesim nuqtalari klassik holi uchun ko’chish grafigi tasvirlangan. 3.4-rasmda i=25 va i=50 qadamga mos keluvchi kesim nuqtalari aniqlashtirilgan tebranish tenglamalari asosida ko’chish vaqtdan bog’liq grafigi tasvirlangan. Bu natijalar bo’yicha va qurilgan grafiklar asosida quyidagi mexanik xulosalarni chiqarish mumkin. 1. Tenglamalarning klassik hol uchun olingan natijalar xususiy holda sterjen uchun olingan natijalarga aynan mos keladi. 2. Ko’ndalang kesimlarda aylanish inersiyasining ta’siri tebranish amplitudalarini 20% gacha kamayishiga olib keladi; 3. Qobiq kesimlaridagi ko’chishlar amplitudalarini kamayishiga olib keladi. (3.4-rasm). Aylanish inersiyasi ta’siri hisobga olinganda bu kattalik klassik holdagiga nisbatan 2-3 barobar katta bo’ladi. 4. Aylanish inersiyasini ta’siri tebranishlarni koordinata bo’yicha asta sekin so’nib borishiga olib keladi. 55 tU i =25 Aylanish inersiyasi i =50 Aylanish inersiyasi § 3.2 Doiraviy elastik silindrik qobiqning buralma tebranish tenglamalarida ko’ndalang siljish deformatsiyasi ta’sirini hisobga olish Doiraviy elastik silindrik qobiq uchun keltirilgan tenglamalarda ko’ndalang siljish deformatsiyasi ta’sirini hisobga olganda (3.6) va (3.7) tenglamalar uchun boshlang’ich va chegaraviy shartlardan foiydalangan holda ,,Paskal” dasturlash tilida tuzilgan dastur asosida ko’chishlar to’rning tugun nuqtalaridagi sonli qiymatlarini aniqlaymiz. Olingan natijalarni grafik ko’rinishida tasvirlaymiz. 3.5-rasm Olingan natijalar buralma ko’chishning vaqtdan bog’liq grafigi ko’rinishida tasvirlangan. 3.5-rasmda i=25 va i=50 (z bo’yicha) qadamga mos keluvchi kesim nuqtalarining ko’chish grafigi klassik va aniqlashtirilgan tenglamalada ko’ndalang siljish deformatsiyasi ta’siri hisobga olingan hol uchun tasvirlangan. 56Klassik i =25 Klassik i =50 Ko’ndalang siljish deformatsiyasi i =25 Ko’ndalang siljish deformatsiyasi i =50tU Hisob ishlarida qobiq materialini po’lat deb qabul qilamiz va mexanik xarakteristikalarini quyidagicha olamiz: . O’rab turuvchi muhitni tuproq deb qaraymiz. Hisob ishlarida tuproqning suglinok va glina bo’lgan hollaridan foydalanamiz. Suglinok uchun 3 , glina uchun ko’rinishida tanlaymiz. h=0,1; Po’lat+Suglinok 3.6-rasm h=0,1; Po’lat+Glina 3.7-rasm 57 ASOSIY XULOSALAR Dissertatsiyta ishi doirasida olingan asosiy natijalar quyidagilardan iborat . 1. Doiraviy elastik sterjening buralma tebranishi umumiy teglamalari keltirib chiqarildi. Olingan umumiy teglamalardan xususiy holda klassik va aniqlashtirilgan tenglamalar kelib chiqishi asoslandi. 2. Doiraviy elastik sterjen ko’ndalang kesimlari aylanish inersiyasini hisobga oluvchi buralma tebranish aniqlashtirilgan tenglamasi taklif qilindi. 3. Doiraviy elastik silindrik qobiq uchun buralma tebranishlari umumiy tenglamalar keltirib chiqarildi. 4. Qobiq uchun chiqarilgan umumiy tenglamalarda aylanish inersiyasi va ko’ndalang siljish deformatsiyasi ta’sirini hisobga olib sonli natijalar olindi. 5. Qobiq uchun chiqarilgan umumiy tenglamalarda aylanish inersiyasi ta’siri hisobga olingan holi uchun natijalar olindi. Ushbu natijalar sterjen uchun xususiy holda qarab chiqilgan natijalarga mos kelishi tekshirildi. 6. Qobiq uchun chiqarilgan umumiy tenglamalarda ko’ndalang siljish deformatsiyasi ta’siri hisobga olingan hol uchun sonli natijalar olindi. 7. O’rab turuvchi muhit suglinok bo’lganda muhit ta’siri tebranishlar amplitudasini 15% gacha kamaytirishga olib keladi. 8. O’rab turuvchi muhit glina bo’lganda muhit ta’siri tebranishlar amplitudasini 25% gacha kamaytirishga olib keladi. 58 FOYDALANILGAN ADABIYOTLAR RO ’ YXATI 1. Филиппов И. Г, Чебан В. Г.Математическая теорS колебаний упругих и вязкоупругих пласт. и стержней. –Киш.ев:Шт.ца, 1988. – 190 с. 2. Худойназаров Х.Х.-Нестационарное взаимодействие цил.дрических оболочек и стержней с деформируемой средой. 3. Х уд о йназаров Х . Продольно-радиальные колебанS круговой цил.дрической вязкоупругой оболочки, находящейся в деформируемой среде//Проблемы д.амики взаимодействS деформируемых сред. Материалы III Всесоюзной конференци.Горис. 4-8 июня 1990 г.-Ереван: 1990.-С.21-26. 4. Бердиев Ш.Д. Продольно-радиальные колебанS цил.дрической оболочки с учетом окружающей среды // Узб. Журнал Проблемы механики – 1998. №1.- С .22-27 5. Кубенко B .Д. Нестационарное взаимодействие элементов конструкций со средой.- Киев: Наук. думка, 1979.-188 с. 6. Петрашень Г.И. Проблемы .женерной теори колебаний вырожденных систем // ИсследованS по упругости и пластичности. – Л.: Изд-во ЛГУ, 1966. - №5. – С. 3-33. 7. Уфлянд Я.С. Распространение волн при поперечных колебанSх стержней и пласт.. Прикл. матем. и мех., 1948, 12, №3, 287-300. 8. Кабулов В.К. О волновых уравненSх колебанS балок, пласт. и оболочек. В сб. Вопр. вычесл. матем. Ташкент, АН УзССР, 1963, 104- 139- РЖМех, 1964, 3В195. 9. Худойназаров Х.Х, А.Абдуллаев Эластик назарSси масалалар.и сонли ечиш. СамДУ, Самарқанд, 1995. 59 10. Худойназаров Х. Х. , Исматова Ф. Основные направленS развитS уточненных теорий колебанS цил.дрических оболочек// Сб.науч.работ.-Изд-во СамГУ, 1997г. - С 11. Тюманок А. Неуситановившееся осесимметричное колебани е цил.дрической оболочки, возбуждаемое подвижной нагрузкой// Изв АН ЭССР. т.14.Сер.фK.-мат. и техн.наук.-1985.-№3.-С.414-421. 12. Н3уль У.К. О применимости приближенных теорий при переходных процессах деформации круговых цил.дрических оболочек//Труды VI. Всесоюзной конференци по теори пласт. и оболочек. Баку, 1966.- М.:Наука, 1966.-С.593-599. 13. Гр3олюк Э.И., Селезов И.Т. Неклассические теори колебаний стержней, пласт. и оболочек // Итоги науки и техники. Сер. Механика тверд. деформир.тел.-Т.5.-М.: ВИНИТИ, 1973.-272 с. 14. ТеорS оболочек с учетом поперечного сдв3а. Под. ред.проф. Галимова К.З.-Казан ь : Kд-во КГУ, 1977.-212 с. 15. Herrmann G., Mirsky I. Iherr-dimensional and shell-theory analysis of xially Summetric motions of cylinders //I.Appl.Mech.-1956.-V.23,№4.-p.563-568. 16. Филлипов И.Г., Кудайназаров К. Приближенные уравненS нестационарных колебаний толстостенной круговой цил.дрической вязкоупругой оболочки// Изв.АН УзССР. Сер.техн.наук.-1980.- №2.С.41-45. 60 17. Шавелев А.А. Вынужденные колебанS консольной цил.дрической оболочки переменной тольщины при к.ематическом возбуждени вдоль оси // Деп. В ЦНИИТЭИ приборстроенS .-№3427. пр . от 10.09.1986 18.Berkowitz H.M. Lonqitudinal impact of a seminfinite Elastic Cylendrical shells // J. Appl. Mech.-1963.-v.30, №3.-P.347-354 19. Ильясов М.Х., Гасанов А.Х. Нес т ационарная задача о продольном ударе по вязкоупругому цил.дрической конечной дл.ы//Изв.АН АзССР. Сер.фK.-техн. и мат. наук.-1986.-7.-№3.-С.50-57. 20.Клейн Г.К. Расчет подземных трубопроводов.-М.: Изд-во Литер. по стр-ву, 1969.-240с. 21. Тимошенко С.П., Янг Д.Х., Уивер У. КолебанS в .женерном деле. Пер. с анг.-М.: Маш.остроение, 1985.-472 с. 22. Исмайилов К. Сиқилган стерженлар, пласт.калар ва қобиқларн.г эластиклик чегарасидан кей.ги устиворл3и. Тошкент, 2006, 175 б. 61 Ilovalar “ Doiraviy elastik qobiqning buralma tebranish tenglamalarida aylanish inersiyasi ta’sirinini hisobga olish” Program Nomozov Q._aylanish_inersiyasi; Uses crt; const Nz=99; Nt=200; jt=200; kt=10; type ff = text; vec1 = array [0..Nz+1] of real; var i,j,k,n,it : integer; u1,u2,u3,x,y,ck,dk,fk,mk,nk,szt,s : vec1; l,d,ta,d2,ta2,t,t0,t1, al1,al0,bet0,bet1,Ab,Bb,r0,ak,gam,eta,gam1,eta1,Dat, ksi1,ksi2,ksi3,a1,a2,a3 ,AL : real; w1,sigma,tn: array[1..100] of real; fl,fli : text; procedure prog3(var y : vec1); begin ck[0]:=al1/(al0*d-al1); dk[0]:=d*Ab/al1; for i:=1 to Nz do begin ck[i]:=1/(mk[i]-nk[i]*ck[i-1]); dk[i]:=fk[i]-nk[i]*ck[i-1]*dk[i-1]; end; y[Nz+1]:=(Bb*d+bet1*ck[Nz]*dk[Nz])/(bet0*d+bet1*(ck[Nz]+1)); i:=Nz+1; while i>=1 do begin i:=i-1; y[i]:=ck[i]*(dk[i]-y[i+1]); end; end; 62 function f(t,t1:real): real; var pi: real; begin pi:=3.14159; if t<=t1 then f:=sin(pi*t/t1) else f:=0; end; begin clrscr; assign(fl,'nom.dat'); rewrite(fl); assign(fli,' nom.dat'); rewrite(fli); {Boshlang'ich ma'lumotlar} l:=10; r0:=1; gam:=0.498; eta:=1-gam; Dat:=0; AL:=0; a1:=0.6; a2:=0.3; a3:=0.1; ksi1:=0.1; ksi2:=0.3; ksi3:=0.6; {Boshlang'ich hisoblar} d:=l/(Nz+1); ta:=0.5*d; d2:=d*d; ta2:=ta*ta; t1:=Nt*ta/4; {Boshlang'ich shartlar} for i:=0 to Nz+1 do begin x[i]:=i*d; u1[i]:=0; u2[i]:=0; u3[i]:=0; s[i]:=0 end; t:=0; j:=0; k:=0;n:=0; for it:=1 to Nt do begin t:=t+ta; {Tenglamani yechish} for i:=0 to Nz+1 do begin {Hamma hadlarda ikkiga ajratish} s[i]:=s[i]+AL*ta*(a1/ksi1*exp(-ta/ksi1)+a2/ksi2*exp(-ta/ksi2)+ a3/ksi3*exp(-ta/ksi3))*(u2[i+1]-2*u2[i]+u2[i-1])*ta2/d2; 63 ak:=-gam/d2-Dat*(1-2*gam)/(6*d2*ta2); mk[i]:=(1/ta2+2*gam/d2+Dat*(1-2*gam)/(3*d2*ta2))/ak; nk[i]:=1; fk[i]:=(-s[i]+1/ta2*(2*u2[i]-u1[i])+eta/d2*(u1[i+1]-2*u1[i]+u1[i-1])+ Dat*(1-2*eta)/(6*d2*ta2)*(u1[i+1]-2*u1[i]+u1[i-1]))/ak; end; al0:=1; al1:=1; bet0:=1; bet1:=1; Ab:=f(t,t1); Bb:=0; prog3(u3); {Chegaraviy shartlar} u3[0]:=f(t,t1); u3[Nz+1]:=0; for i:=1 to Nz do begin szt[i]:=(u3[i+1]-u3[i-1])/(2*d); end; for i:=0 to Nz+1 do begin u1[i]:=u2[i]; u2[i]:=u3[i]; end; {Pechat} j:=j+1; k:=k+1; if k=kt then begin k:=0; n:=n+1;tn[n]:=t; w1[n]:=u3[10]; end; if j=jt then begin j:=0; for i:=0 to Nz+1 do begin writeln(x[i]:10:5,' ',u3[i]:10:5); writeln(fl,x[i]:10:5,' ',u3[i]:10:5); end; end; end; 64 close(fl); for i:=1 to n do writeln(fli, tn[i]:10:4,' ',w1[i]:10:5); close(fli); end. Doiraviy elastik silindrik qobiqning buralma tebranish tenglamalarida ko’ndalang siljish deformatsiyasi ta’sirini hisobga olish Program Nomozov_Q_ko’ndalang siljish; Uses crt; const Nz=99; Nt=100; jt=100; kt=2; type ff = text; vec1 = array [0..Nz+1] of real; var i,j,k,n,it : integer; u1,u2,u3,v1,v2,v3,x,y,ck,dk,fk,mk,nk,szt : vec1; l,d,ta,d2,ta2,t,t0,t1, al1,al0,bet0,bet1,Ab,Bb,r0,ak,gam,eta,gam1,eta1,omega,o mega2, mu,mu1, r1,r2,co,e,nu,aco,bco,cco,kco,dco,qo, a1,a2,s1,s2,s3,s4,k1,k2,k3,k4 : real; w1,w2,w3,sigma,tn: array[1..100] of real; fl,fli : text; procedure prog3(var y : vec1); begin ck[0]:=al1/(al0*d-al1); dk[0]:=d*Ab/al1; for i:=1 to Nz do begin ck[i]:=1/(mk[i]-nk[i]*ck[i-1]); dk[i]:=fk[i]-nk[i]*ck[i-1]*dk[i-1]; end; y[Nz+1]:=(Bb*d+bet1*ck[Nz]*dk[Nz])/(bet0*d+bet1*(ck[Nz] +1)); i:=Nz+1; while i>=1 do begin i:=i-1; y[i]:=ck[i]*(dk[i]- y[i+1]); end; end; function f(t,t1:real): real; var pi: real; begin 65 pi:=3.14159; if t<=t1 then f:=sin(pi*t/t1) else f:=0; end; begin clrscr; assign(fl,'BerdZ.dat'); rewrite(fl); assign(fli,'BerdT.dat'); rewrite(fli); {Boshlang'ich ma'lumotlar} l:=10; r0:=1; gam:=0.5; eta:=1-gam; omega:=0.2; omega2:=omega*omega; mu:=1; mu1:=1.5; {Boshlang'ich hisoblar} d:=l/(Nz+1); ta:=0.8*d; d2:=d*d; ta2:=ta*ta; t1:=Nt*ta/4; {Boshlang'ich shartlar} for i:=0 to Nz+1 do begin x[i]:=i*d; u1[i]:=0; u2[i]:=0; u3[i]:=0; v1[i]:=0; v2[i]:=0; v3[i]:=0 end; e:=2.0e11; nu:=0.3; mu:=e/(2*(1+nu)); r1:=1; r2:=1.1; a1:=1; a2:=1; co:=2*(1+nu); S1:=2*co*(sqr(sqr(r2))-sqr(sqr(r1)))/(sqr(r1*r2)*ln(r2/ r1)); S4:=16/(sqr(sqr(r1))+sqr(sqr(r2))); S3:=(sqr(r2)-sqr(r1))/(sqr(r1*r2)*ln(r2/r1)); S2:=32*(sqr(sqr(r2))-sqr(sqr(r1)))/(sqr(sqr(r1*r2))*ln( r2/r1)); aco:=-e/mu/(a1*co); bco:=(a2*co+a1*e/mu)/(a1*co); cco:=S1*S4/(a1*co)/100; dco:=-S3*e/mu/(a1*co); kco:=-S2*e/mu/(a1*co); k1:=bco/d2; k2:=aco/sqr(d2); k3:=dco/d2; k4:=cco; j:=0; 66 t:=0; j:=0; k:=0;n:=0; for it:=1 to Nt do begin t:=t+ta; {Tenglamani yechish} for i:=0 to Nz+1 do begin {Hamma hadlarda ikkiga ajratish} ak:=-gam/d2; mk[i]:=(1/ta2+2*gam/d2-cco)/ak; nk[i]:=1; qo:=dco/d2*(v2[i+1]-2*v2[i]+v2[i-1])+kco*v2[i]; fk[i]:=(1/ta2*(2*u2[i]-u1[i])+eta/d2*(u1[i+1]- 2*u1[i]+u1[i-1])+ cco*u2[i-1]+qo)/ak; end; al0:=1; al1:=1; bet0:=1; bet1:=1; Ab:=f(t,t1); Bb:=0; prog3(u3); {Chegaraviy shartlar} u3[0]:=f(t,t1); u3[Nz+1]:=0; for i:=0 to Nz+1 do begin szt[i]:=(u3[i+1]-u3[i-1])/(2*d); v3[i]:=2*v2[i]-v1[i]+ta2*u3[i]; end; for i:=0 to Nz+1 do begin u1[i]:=u2[i]; u2[i]:=u3[i]; v1[i]:=v2[i]; v2[i]:=v3[i]; end; {Pechat} j:=j+1; k:=k+1; if k=kt then begin k:=0; n:=n+1;tn[n]:=t; w1[n]:=u3[25]; w2[n]:=u3[50]; w3[n]:=u3[75]; end; if j=jt then begin j:=0; for i:=0 to Nz+1 do begin writeln(x[i]:10:5,' ',u3[i]:10:5); writeln(fl,x[i]:10:5,' ',u3[i]:10:5); end; end; 67 end; close(fl); for i:=1 to n do writeln(fli,tn[i]:10:4,w1[i]:10:5,w2[i]:10:5,w3[i]:10:5 ); close(fli); end. 68

DEFORMATSIYALANUVCHI MUHITDA JOYLASHGAN SILINDRIK QOBIQNING BURALMA TEBRANISHLARIGA AYLANISH INERSIYASI VA KO’NDALANG SILJISH DEFORMATSIYASI TA’SIRI MUNDARIJA KIRISH........................................................................... ...............3 I-BOB. DOIRAVIY ELASTIK STERJEN BURALMA TEBRANISHI ASOSIY TENGLAMALARI. §1.1 Doiraviy elastik silindrik sterjenning vaqtdan bog’liq tebranishlari .................................................................................9 §1.2 Doiraviy elastik silindrik sterjenning buralma tebranishi umumiy tenglamalari.................................................................................16 §1.3 Doiraviy silindrik qobiqning buralma tebranishlarida deformarsiyalanuvchi muhit ta’sirini e’tiborga olish..................26 §1.4 Doiraviy elastik silindrik sterjenning buralma tebranishlari asosiy tenglamalari (xususiy hol)...........................................................33 II-BOB DIFFERENSIAL TENGLAMALARNI YECHISHNING SONLI USULLARI §2.1 С hekli ayirmalar usulini d ifferentsial tenglamalar yechishda qo’llanilishi..................................................................................37 §2.2 Differentsial tenglamalarni taqribiy yechish ….........................45 III-BOB DOIRAVIY ELASTIK SILINDRIK QOBIQNING BURALMA TEBRANISHLARI §3.1 Doiraviy elastik silindrik qobiqning buralma tebranish tenglamalarida aylanish inersiyasi ta’siri ...................................51 §3.2 Doiraviy elastik silindrik qobiqning buralma tebranish tenglamalarida ko’ndalang siljish deformatsiyasi ta’siri............................................................................................58 XULOSA…...………..…………………………………………60

FOYDALANILGAN ADABIYOTLAR RO’YXATI……….....61 Ilovalar.........................................................................................64 Kirish Keyingi vaqtlarda fan va texnikaning jadal rivojlanishi turli xil yangi t urdagi konstruksiya elementlarini yangi tex nologiyalar asosida yaratishga olib kelmoqda. Hozirgi zamon texnikasi tez sur’atlar bilan rivojlanishi mexanika sohasida qilinishi kerak bo’lgan yangidan-yangi, nazariy va amaliy masalalarni yechishni qo’ymoqda. Keyingi yillarda materiallar yuqori bosimli va yuqori haroratli o’ta murakkab jarayonlarda qo’llanilmoqda. Materiallar chidamli, mustahkam va arzon bo’lishi uchun ularning qotishmalaridan o’ta mustahkam va yaroqli modulli tolalar amaliyotda keng qo’llanilmoqda. Bunday yangiliklar jismning elastiklik modeli bilan bir qatorda, deformatsiyalanuvchi qattiq jismning boshqa, umumiyroq va mukammalroq modellarini ham yaratishga olib keldi va bu modellardan keng miqyosda foydalanilmoqda. Bunda jismlarning plastiklik, qovushoq-elastiklik xususiyatlaridan keng ko’lamda foydalanishga olib kelmoqda. Keyingi yillar davomida deformatsiyalanuvchi qattiq jismlar mexanikasining “yemirilish mexanikasi”, “kompozit materiallar mexanikasi”, “Nanomexanika” va shu kabi qator yangi yo’nalishlar paydo bo’lishiga ham ana shu yangi talablar sabab bo’ladi. Ushbu yangiliklar zamirida eng avvalo elastik jism modeli yotadi. Dissertatsiya ishining tadqiqot predmeti t ashqi ta’sir natijasida konstrukksiya elementlari sterjenlar, plastinka va qobiqlarda paydo bo’ladigan tebranish turlarini aniqlash. Tebranishlar vaqtdan bog’liq xususiyatga ega bo’lgan hollarda bunday elementlarda paydo bo’ladigan nostatsionar to’lqinlar tarqalish jarayonlarini, ularning fizik-mexanik xususiyatlarini hisobga olgan holda tadqiq qilishdan iborat. Vaqtdan bog’liq tebranishlarni o’rganishda tebranishlarning xususiy chastotalari, xususiy amplitudalarini aniqlash va tebranish formalarini topish masalalarini qo’yish, ularni yechish va ilmiy xulosalar chiqarish. 2

Qobiqlarlar nostatsionar tebranishlarni tashqi dinamik yuklar ta’sirida uyg’otilgan hollar uchun fizik-mexanik xarakteristikalardan foydalanib tadqiq etish dissertatsiya ishining predmetini tashkil etadi. Dissertatsiya ishining tadqiqot ob’ekti yuqorida aytib o’tilgan xulosalardan foydalanib, ko’ndalang kesimi doiraviy, uzunligi chekli, materiali elastik bo’lgan silindrik qobiq va qatlamlar qaralgan. Bunda qobiqlarning buralma tebranishlarida hosil bo’ladigan kuchlanganlik-deformatsiyalanganlik holatini qatlam materialining fizik-mexanik xususiyatini e’tiborga olgan holda aniqlash mumkin. Bulardan tashqari qobiqni o’rab turuvchi asosiy ob’yekt tariqasida deformatsiyalanuvchi muhit ta’siri ham e’tiborga olingan. Mavzuning dolzarbligi doiraviy elastik qobiqlar mexanika sohasining juda ko’p va xilma-xil muhandislik qurilmalari tarkibiy qismlarini tashkil qiladi.Bunday qobiq va qatlamlar ko’plab mashina va mexanizmlarning asosiy elementlari hisoblanadi. Demak o’z-o’zidan ko’rinadiki bunday qobiq va qatlamlar turli xil dinamik tashqi ta’sirlar ostida bo’ladi va ularning ko’ndalang kesimlarida har xil yuklanishlar paydo bo’ladi. Sterjenlardagi bunday yuklanishlarni aniqlash masalasi deformatsiyalanuvchi qattiq jismlar mexanikasining dolzarb masalalaridan biri hisoblanadi. Tashqi ta’sirlar ostidagi qobiq va qatlamlar ko’ndalang kesimlaridagi kuchlanganlik-deformatsiyalanganlik holatlarini aniqlash dolzarb hisoblanadi. Bunda, tashqi dinamik ta’sirlar natijasida qatlam nuqtalarida paydo bo’ladigan kuchlanganlik-deformatsiyalanganlik holatlarini aniqlash murakkablashadi. Bunday hollarda masalani analitik yechish mumkin bo’lmay qoladi va masalani yechishda sonli usullardan foydalanishga to’g’ri keladi. Shulardan kelib chiqqan holda dissertatsiya doirasida qaralgan masala dolzarb masalalar qatoriga kiradi deb hisoblash mumkin. Deformatsiyalanuvchi qattiq jismlar mexanikasi masalalarini sonli yechishda qo’llanilib kelinayotgan usullardan chekli elementlar, chekli ayirmalar va chegaraviy elementlar usullarini keltirishimiz mumkin. Bunday usullardan biri sifatida dissertatsiya doirasida chekli ayirmalar usulidan foydalanamiz. Bundan 3

tashqari qaralayotgan masalalarni yechishda ularning matematik modelini qurishda asosiy omil sidatida [1, 2] ishlarining natijalaridan foydalanamiz. Ishning maqsad va vazifalari magistrlik dissertatsiyasi ishining asosiy maqsadi qilib ko’ndalang kesimi doiraviy bo’lgan elastik silindrik qobiq va qatlamlarning vaqtdan bog’liq buralma tebranishlarini tadqiq qilish, tenglamalarda aylanish inersiyasi hamda ko’ndalang siljish deformatsiyasi ta’sirlarini inobatga olish etib belgilangan. Bunda tadqiqotni klassik va aniqlashtirilgan [3,4] tebranish tenglamalari asosida olib borish va masalalarni sonli usullar yordamida yechish vazifasi qo’yilgan. Yuqorida keltirib o’tilganlardan kelib chiqib dissertatsiya ishining asosiy vazifalari qilib quyidagilar belgilangan:  elastiklik nazariyasi asosiy tenglama va munosabatlarini tahlil qilish;  ko’ndalang kesimi doiraviy elastik qobiq va qatlamlar uchun buralma tebranish umumiy tenglamalarini keltirib chiqarish;  klassik va aniqlashtirilgan tebranish tenglamalarini xususiy hollarda keltirib chiqarish;  differensial tenglamalarni yechishning sonli usullarinini tahlil qilish;  chekli ayirmalar va progonka usullarini o’rganish hamda amaliy masalalar yechishga tadbiq etish;  Olingan natijalar asosida ilmiy xulosalar chiqarish. Muammoning ishlab chiqilish darajasi. Doiraviy elastik sterjen va qobiqlarda buralma tebranishlarni tadqiq etish masalasi bilan juda ko’p olimlar shug’illanishgan va hozirgacha ilmiy izlanishlar olib borishmoqdalar. Fan va texnikaning taraqqiyot darajasi materiallarning yangidan-yangi xususiyatlarini, jumladan: reologik, anizotropik, temperaturaviy va h.k. xususiyatlarini inobatga olgan holda tadqiqotlar olib borishni talab etmoqda. Bundan tashqari sterjenlardagi buralma tebranishlarni yangi aniqlashtirilgan tebranish tenglamalar asosida keltirib chiqarish bo’yicha juda kam ishlar bajarilgan. Tadqiqotning ilmiy yangiligi. Doiraviy elastik silindrik qobiqlarning buralma tebranishlari haqidagi masalalar analitik yechimlar asosida tadqiq etilgan. 4

Aslida dinamik jarayonlarda bu kabi yechimlarni olish juda murakkab hisoblanadi. Bunda ko’proq xotira effektini hisobga oladigan aniqroq ravishda natija beradigan singulyar yadrolardan foydalaniladi. Bu kabi yadrolar bilan esa masalani analitik yechish qiyinlashadi yoki masalani yechib bo’lmaydi. Shuning uchun sterjen va qobiqlarning buralma tebranishlari haqidagi masalalarni sonli tadqiq etish talab etiladi. Sonli usullardan foydalanish hozirgi vaqtla katta ilmiy va amaliy ahamiyatga ega bo’lmoqda. Maskur dissertatsiya ishi doirasida qaralgan va yechilishi uchun sonli usullar tadbiq etilgan masalalarning ilmiy ahamiyati birinchidan, materialning elastiklik xususiyati hisobga olinganligi ikkinchidan, masalani yechish uchun chekli ayirmalar usulining qo’llanilishidan iboratdir. Dissertatsiya ishining ilmiy yangiligi doiraviy elastik qobiqning buralma tebranishi uchun tebranish tenglamalariga sonli usullarning qo’llanilishidan iboratdir. Tadqiqotning amaliy ahamiyati. Hozirgi zamon texnikasi, yer osti va yer usti inshootlari, qurilish, aviatsiya, kemasozlik va boshqa juda ko’plab sohalarda ko’ndalang kesimi doiraviy bo’lgan qobiq va qatlamlar muhandislik qurilmalarining asosiy elementlaridan biri sifatida ishlatiladi. Qo’llanilish jarayonida bunday qatlamlar intensiv va impulsli dinamik yuklar ta’siri ostida bo’ladilar. Ko’p hollarda ularning dinamik chidamlilik darajasini tajribadan emas, balki hisoblash ishlari yordamida aniqlashga to’g’ri keladi. Yuqorida keltirilganlar elastik doiraviy qatlamlarning vaqtdan bog’liq tebranishlarini tadqiq qilish, ularning tebranish chastotasi va amplitudasi, tebranishlar shakli, ko’chishi va kuchlanishi kabi boshqa xarakteristikalarini aniqlash tadqiqotning amaliy ahamiyatga ega ekanligidan dalolatdir. Dissertatsiya ishida qaralgan qobiq va qatlamlarning buralma tebranishlari haqidagi masalalar ham shunday tadqiqotlar sarasiga kiradi va muhim amaliy ahamiyatga ega bo’lgan masalalardan biri ekanligini ko’rsatadi. Dissertatsiya ishining tuzilishi. Ushbu magistrlik dissertatsiyasi ishi kirish, uchta bob, xulosa va foydalanilgan asosiy adabiyotlar ro’yxatidan iborat bo’lib jami … .betni tashkil qiladi. 5

O'xshashlar

BIR CHETI BIKR MAHKAMLANGAN IKKINCHISI SHARNIRLI TAYANGAN IKKI QATLAMLI PLASTINKANING SIMMETRIK TEBRANISHLARI
DOIRAVIY SILINDRIK ELASTIK STERJENNING NOCHIZIQLI BURALMA TEBRANISHI
CHETLARI SHARNIRLI MAHKAMLANGAN UCH QATLAMLI QOVUSHOQ-ELASTIK PLASTINKANING SIMMETRIK TEBRANISHI
QISQA MUDDATLI DINAMIK YUKLANISHLAR TA’SIRIDA QOVURG`ALI ELASTIK-PLASTIK YASSI QOBIQNINIG NOCHIZIQLI DEFORMATSIYALANISHI
CHETLARI BIKR MAHKAMLANGAN IKKI QATLAMLI PLASTINKANING SIMMETRIK TEBRANISHLARI