Tengsizliklarni isbotlashni ba’zi usullari














“ Tengsizliklarni isbotlashni ba’zi usullari’’
Mundare ja: 1-Bob. SON LI TEN GSIZLI KLA R 1.1.SoNLI TENGSIZLIKLAR VA ULARNING UMUMIY XOSSALARI. 1.2.SONLI TENGSIZLIKLARGA OID OLIMPIADA MASALALARI ISBOTI. 2-Bob. O’RTA QIY MATLAR VA ULAR O’RTASIDAGI MUN OSA BATLA R 2.1. O’rta qiymatlar orasidagi munosabatlarning geometrik ma’noda isbotlari. 2.2. Koshi tengsizligi va uning turli xil isbotlari . 2.3. Koshi tengsizligi yordamida olimpiada tengsizliklarini yechish. 3-Bob. KOSHI-SHVARS TEN GSIZLI GI VA N OSTAN DART TEN GSI ZLI KLAR 3.1. Koshi –Shvars tengsizligi va uning turli isbotlari 3.2. Koshi –Shvars tengsizligi yordamida olimpiada masalalarini yechish 3.3.Nostandart tengsizliklar va ularning turli xil isbotlari 3.4. Mustaqil yechish uchun masalalar Xulosa. Foydalanilgan adabiyotlar.
Kirish Masalaning dolzarbligi . Ushbu malakaviy bitiruv ishi tengsizliklar va ularning turli xil isbotlarini o’rganish bilan bag’ishlanadi . Tengsizliklarni isbotlashning yangi samarali usullari va ularni qo’llanishiga doir turli matematik olimpiadalardagi masalalar keltirilgan. Umumiy o’rta ta’lim maktablari, akademik litseylar va kasb–hunar kollejlarining iqtidorli o’quvchilari, matematika fani o’qituvchilari hamda pedagogika oliy o’quv yurtlari talabalari uchun mo’ljallangan. Qo’llanmadan sinfdan tashqari mashg’ulotlarda, o’quvchilarni turli matematik musobaqalarga tayyorlash jarayonida foydalanish mumkin. Masalaning qo'y ilishi . Malakaviy bitiruv ishida Sonli tengsizliklar va ularning umumiy xossalari va ularga oida olimpiada tengsizliklari yechimlaridan namunalar ,O’rta qiymatlar va ular orasidagi bir nechta munosabatlar va Koshi tengsizligi uning isboti va unga oid bir nechta murakkab olimpiada masalalari ,
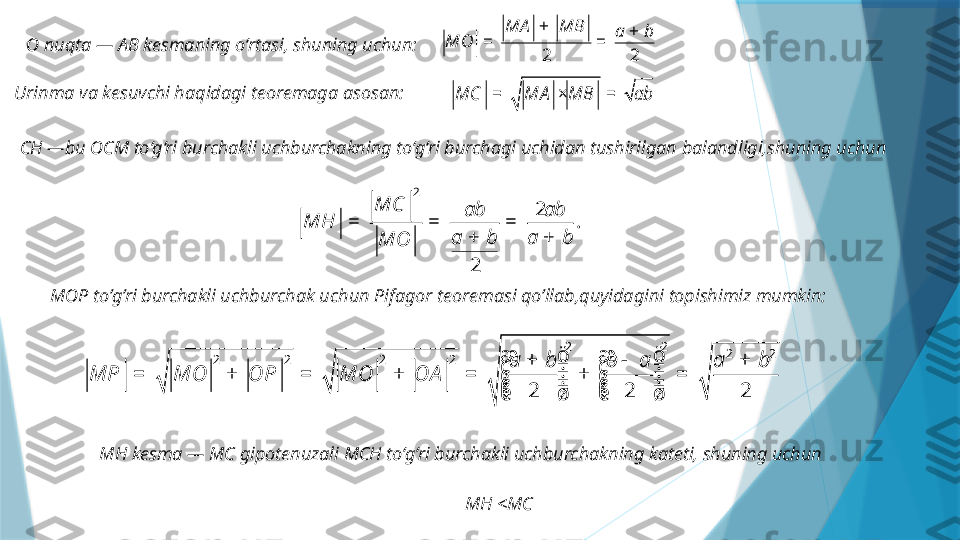
Klassik t engsizlik larning geomet rik manosi. 1.Masal a. M nuqta O markazli aylanadan tashqarida yotibdi. OM to‘g‘ri chiziq aylanani A va B nuqtalarda kesib o‘tadi. M nuqtadan o‘tuvchi to‘g‘ri chiziq aylanaga C nuqtada urinadi. H nuqta — C nuqtaning AB dagi proyeksiyasi, AB ga O nuqtada o‘tkazilgan perpendikulyar aylanani P nuqtada kesib o‘tadi. MA =a va MB =b ekani ma’lum. MO , MC , MH , MP larni toping va o‘sish tartibida yozing. Ye chish : Aniqlik uchun a<b deb qabul qilib olamiz .
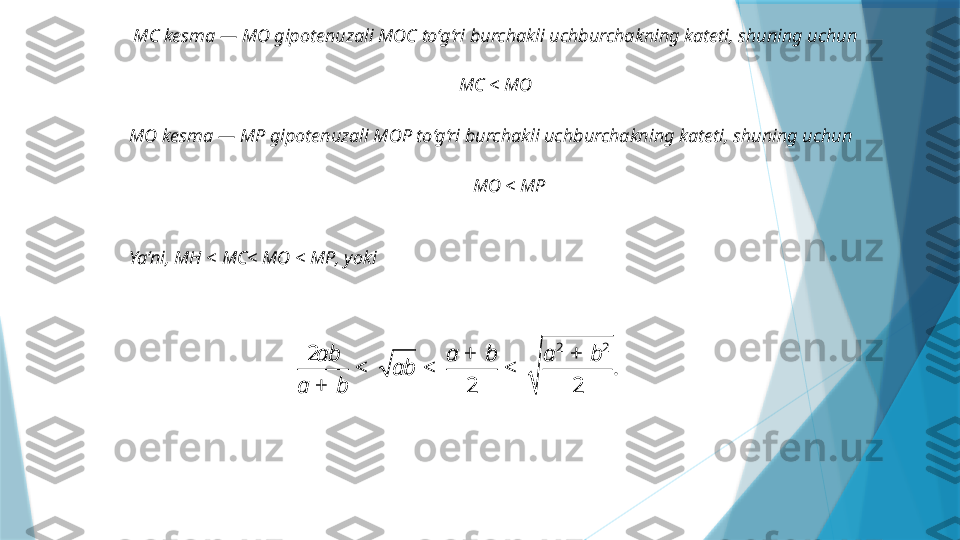
O nuqta — AB kesmaning o‘rtasi, shuning uchun: 2 2MA MB a b MO + + = = Urinma va kesuvchi haqidagi teoremaga asosan:MC MA MB ab = × = CH —bu OCM to‘g‘ri burchakli uchburchakning to‘g‘ri burchagi uchidan tushirilgan balandligi,shuning uchun 2 2 . 2 MC ab ab MH a b a b MO = = = + + MOP to’g’ri burchakli uchburchak uchun Pifagor teoremasi qo’llab,quyidagini topishimiz mumkin: 2 2 2 2 2 2 2 2 2 2 2 a b b a a b MP MO OP MO OA æ ö æ ö + - + ÷ ÷ ç ç ÷ ÷ = + = + = + = ç ç ÷ ÷ ç ç ÷ ÷ ç çè ø è ø MH kesma — MC gipotenuzali MCH to‘g‘ri burchakli uchburchakning kateti, shuning uchun MH <MC
