CHekli ayirmali usullar. Adamsning ekstropolyatsiya formulasi Adamsning interpolyatsiya formulasi. Miln ,Runge-Kutta qadamli usuli




![yechimlari to`g`ri kelishini ko`rsatamiz. Buni karrali ildizlar haqiqiy bo`lgan hol
uchun qarash bilan kifoyalanamiz, chunki aytilgan gaplar kompleks bo`lgan hol
uchun ham o`rinlidir.
Xarakteristik kop`hadni ko`paytuvchilarga ajratamiz:∑
i=0
p
aiλi=ap∏
i=1
p
(λ− λ1)
Haqiqiy
ε>0, ε→ 0 parametrni olib, quyidagi ikki shartni qanoatlantiruvchi
λiε
ni olamiz:
1) barcha i = 1,2,..., k uchun
λiε lar har xil;
2) barcha i
¿ кuchun limx→0λiε= λi
Bu ildizlarga moc keladigan xarakteristik tenglamani tuzamiz:
0=ap∏
i=1
p
(λ− λiε)=∑
i=0
p
aiελi
Ko`rinib turibdiki,
limx→0aiε=ai Bu xarakteristik tenglamaga
∑
i=0
p
aiεzn+1=0
(1.12)
ayirmali tenglama mos keladi. Endi faraz qilaylik
ε > 0 uchun [1.12] tenglamaning
shunday
zε,n yechimini ko`rsata olaylikki, ixtiyoriy п> 0uchun limε→0zε,n=zn limit
mavjud bo`lsin. Agar
limε→0aiε=ai ni hisobga olib, (1.12) tenglamada limitga o`tsak u
holda zn limitdagi funksiya (1.10) tenglamaning yechimi ekanligini ko`ramiz.
Shunday ketma-ket-liklarni ko`ramizki, ular (1.10) tenglamaning karrali ildiziga
mos keladigan xususiy yechimiga yaqinlashsin. Bunday qurishni amalga oshirish
uchun bo`lingan ayirmalardan foydalanamiz. Avval ildiz ikki karrali bo`lgan holni
ko`ramiz, buning uchun
ϕ(λ)= λn deb belgilab,
z2ε,n=ϕ(λ1ε,λ2ε)= λ2εn− λ1εn
λ2ε− λ2ε
birinchi tartibli bo`lingan ayirmani olamiz. Ko`rinib turibdiki, bu funksiya (1.10)
tenglamani qanoatlantiradi. Endi
limε→0λ1ε= limε→0λ2ε= λ1 ni hisobga olib, limitga
o`tamiz:
limε→0z2ε,n=limε→0(λ2εn−1+λ2εn−2λ1ε+...+λ1εn−1)=nλ 1n−1
Shunday qilib, biz ikki karrali ildizga mos keladigan yana bir yechimga ega
bo`ldik. Endi ning karraligi ikkidan katta bo`lgan holni ko`rib chiqamiz. Buning
uchun 5-bobdagi bo`lingan ayirmalar nazariyasiga oid ikkita formuladan
foydalanamiz:](/data/documents/5f0939a8-d131-4958-888c-6e4aa3bc8e8d/page_5.png)





![Ko’phad t=ϕ(t) ko’rinishiga keltiriladi:
t= y− y0
Δy 0
− Δ2y0
2!Δy 0
t(t−1)−........ bunda
t0=
y− y0
Δy 0
−
boshlang’ich yaqinlashish.
Misol.Ushbu
y=lg x funksiyaning quyidagi qiymatlar jadvali bo’yicha x ning
y=1,35
ga mos qiymati topilsin.
Yechish:
y0=1,3010 ,t0=(y− y0)/Δy 0=(1,35 −1,3010 )/0,0969 =0,506
t1=0,506 +177
2⋅969 ⋅0,506 (0,506 −1)=0,506 −0,023 =0,483
t2=0,506 +177
2⋅969 ⋅0,483 (0,483 −1)=0,506 − 0,023 =0,482
t=0,483 ,x= x0+ih = 20 +0,483 ⋅5= 22 ,42
Har xil uzoqlashgan tugunlar xolida
Ln(x) bo’lingan ayirmali N(x)
va boshqaformulalar qo’llaniladi. Buning uchun formulardagi
x va y joylari
almashtiriladi.
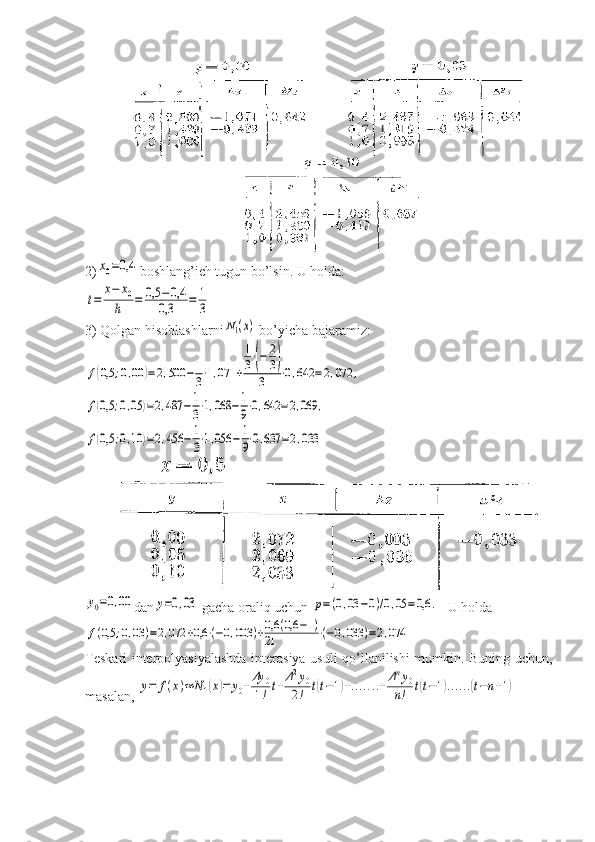
Misol: Ushbu
f(x)= x2+ln x= 0 tenglamaning [0,5,1 ] oraliqda yotgan ildizi topilsin.
Yechish:
f(0,5 )<0, f(1)>0 Qachon h=0.05](/data/documents/5f0939a8-d131-4958-888c-6e4aa3bc8e8d/page_12.png)

![R'n(x)= (−1)n
h
Δn+1y0
n+1 , q=50 −50
h =0,
y'(50 )= 1
5(0,0414 +(−1)
2 ⋅(− 0,0036 )+1
3⋅0,0005 )≈ 0,0087 .Sonli differensiallashda interpolyasiya qadamini kichraytirish formuladagi keying
hadlarni tashlashdan vujudga keladigan xatoni (kesim hatosini) kamaytiradi, lekin
yaxlitlash xatosini oshiradi. Shunga ko’ra umuman, differensiallashning sonli
usullari formulalarning yaqinlashishini taminlay olmaydi.
Splaynlar yordamida funksiyalarni yaqinlashtirish.
[a,b] oraliq [xi−1,xi]
(i=1;)n,x0= a,xn= b
qismlarga ajratilgan bo’lsin. Biror uzluksiz f(x)∈C[a,b]
funksiya uchun m-tartibli interpolyasion polinominal splayn deb, ushbu shartlarni
qanoatlantiruvchi
Sm(x) funksiyaga aytiladi.
1)
[a,b] oraliqning xar bir [xi−1,xi] qismida y m. –darajali Sm(x)= a0+a1x+amxm
ko’phaddan iborat; 2)
[a,b] oraliq bo’yicha m-1-tartibgacha uzluksiz xosilalarga
ega; 3)
xk tugunlarda Sm(x)= a0+a1x+....+amxm ko’phaddan iborat. Agar n→ ∞ da
max
|xi− xi−1|→ 0 bo’lsa, u holda.
S1(x)
splayn f(x)∈C[a,b] funksiyaga tekis yaqinlashadi. Tekis yaqinlashish
xususiyati
S2(x) kvadratik splayn va S3(x) kubik splaynlar uchun ham o’rinli
bo’lib, yaqinlashish tezligi splaynning tartibiga va
f(x) ning silliqligiga muvofiq
ravishda ortadi.
Splaynni tuzish uchun
a0,....,an koeffisientlar aniqlanishi kerak. Chiziqli
S1(x)= a0+a1x
splayinning a0,a1 koeffisientlarini topish uchun f(xi−1) va f(x1)
qiymatlar yetarli. 3) shartga asoslanib ushbu
{
a0+a1xi−1= f(xi−1)(i=¯1;¯n),
a0+a1xi= f(xi)
Sestemani tuzamiz va undan
a0,a1 larni aniqlaymiz. m≥ 2 bo’lgan holda Sm(x) ning
yagona bo’lishini taminlash uchun yana m-1 ta qo’shimcha shart qo’yilishi kerak.
Odatda bunday shartlar [(х) ning yaqinlashish хususiyatlari, splayn ikki qo'shni
bo'lagining tutashgan nuqtalarida silliq bo'lishlari va boshqa talablarga ko'ra,
shuningdek, chetki a va
b nuqtalarda turli chegaraviy shartlar bilan qo'yiladi.
1-masala. Ushbu
s(x)(s(x)∈S1) funksiyalar quyidagi
s(xi)= f(xi),i=¯0,¯n,J1(s)=∫
0
1
(s'(x))2dx <∞](/data/documents/5f0939a8-d131-4958-888c-6e4aa3bc8e8d/page_14.png)
![shartlarni qanoatlantirsin. Bu funksiyalar orasidan shunday S1(x) funksiyani topish
talab qilinadiki, unga ko'ra
inf J1(x)
olinadigan bo'lsin. Bizdan х- nuqtalarda S1(x)
oilaning biror manoda
f(x) bilan bir хil kiymatga ega
bo'lgan va nisbatan silliq funksiyalaridan birini, ya'ni
eng kichik normali funksiyani topish talab etiь
ladi. Ma'lumki,
J=∫
a
b
F(s(x),s'(x))dx aniq integralni maksimum va minimumga
erishtiradigan har qanday
s(x) funksiya
d
dx (
∂F
∂s')− ∂F
∂s=0
Eyler tenglamasini lantirishi kerak. Bizda bu tenglama 5" (.*:) = 0 ko'rinishida.
Sh.unga ko'ra izlanayotgan (х) funksiya har bir [,s. _ ., l-]
oraliqda chiziqlidir. Demak, (х) birinchi tartibli DD-х)
splayndan iborat.
Masala.
|xi−1,xi| (i= ¯1,¯n,x0= a, xn=b) qismlarga ajratilgan [a,b] oraliqda jadval
ko’rinishida berilgan
f(x) funksiyani interpolyasiyalovchi shunday S2(x) kvadratik
splayn tuzilsinki, u uchun yukorida ko'rsatilgan 1) — 3)
shartlar va qo'shimcha 4) shart bajarilsin, ya'ni:
1) Har qaysi
xi−1,xi oraliqda splayn bo’lagi s(x)=a0+a1x+a2x2 ko’rinishidagi
ko’phaddan iborat; 2)
S2(x)=∈C '[a,b]; 3)S2(xk)= fk; 4)x0= a da s'(a)= A har
qaysi
xi=(i=1;n−1 ) nuqtada s'(x− 0)= s'(x+0) tenglik o’rinli bo’sin. Echish:
Splaynning [х, х,] oraliqdagi bo'lagini topish
uchun ko'rsatilgan shartlardan foydalanib ushbu sestemani
tuzamiz:
{
a0+a1x0+a2x02= f0
a0+a1x1+a2x12= f1
a1+2a2x0= A
Sestemani yechib, topilgan
a0, a1 a2 koeffitsientlar bo’yicha izlanayotgan
s(x)=a0+a1x+a2x2
ni tuzamiz.
Turning qolgan har qaysi
|xi−1,xi| (i=2;¯n qismi uchun
{
a0+a1xi−1+a2xi−12 = f(xi−1)
a1+a1xi+a2xi2= f(x)
s'(xi−0)=s'(xi+0)](/data/documents/5f0939a8-d131-4958-888c-6e4aa3bc8e8d/page_15.png)
![Ko’rinishidagi sestema tuziladi va izlanayaotgan s(x)= a0+a1x+a2x2 ko’phad
olinadi, bunda
s'(x)=a1+2a2x
Misol. Biroq
f(x) funksiya f'(0,78 )=−2,5 va
jadval bilan berilgan. Uni interpolyasiyalovchi ikkinchi
tartibli splayn tuzilsin.
Yechish:
[0,78 ;1,56 ] oraliq uchun:
{
a0+0.78 a1+0,78 2a2=2,5 ,
a0+1,56 a1+1,56 2a2=1,2
a1+2⋅0,78 a2=−2,5
Sistemani yechib ,
a2=1,069 ,a1=−4,168 ,a0=5,1 ni topamiz. Izlanayotgan uchhad
s(x)=5,1 −4,168 x+1,069 x2
bo’ladi.
[1,56 :2,34 ]
oraliq uchun: oldingi oraliq uchun topilgan munosabatdan foydalanib,
s’(1,56)=-4,168+2,136*1,56=-0,83 ni aniqlaymiz. So’ng quidagi sistemani
topamiz.
{
a0+0.78 a1+0,78 2a2=2,5 ,
a0+1,56 a1+1,56 2a2=1,2
a1+2⋅0,78 a2=−2,5
Bu sistemadan ,
a2=0,936 ,a1=−3,755 ,a0=4,781 aniqlanadi.
[2,34 :3,12 ]
oraliq uchun:
s’(2,34)=-3,755+2*0,936*2,34=0,625
{
a1+2a2⋅3,12 =−0,833
a0+a1⋅3,12 +3,12 2a2=2,25
a0+3,81 a1+3,81 2a2=4,28
Bundan
a2=0,971 ,a1=−3,787 ,a0=4,614 va
s(x)=4,614-3,787x+0,971x
2
Shunday qilib tuzilishi talab etilayotgan
S3(x) splayn ketma-ket joylashgan xi−1,xi
oraliqlar uchun topilgan s(x) uchhadlar majmuasidan iborat.
3. 1.4. Runge-Kutta usullari Eylerning to‘g‘rilangan usulida ikkinchi tartibli hosila
2 2 ( ) dx d y xi ni olish uchun (1.5) chekli ayirmali formuladan foydalaniladi,](/data/documents/5f0939a8-d131-4958-888c-6e4aa3bc8e8d/page_16.png)

![usullari bu mos ravishda Eyler usuli va uning modifikatsiyalangan usulidir. Yana
bir variant, Koshi masalasini o‘zgarmas h qadamli 4-tartibli aniqlikka ega bo‘lgan
Runge-Kutta usuli bilan yechish formulalari quyidagicha: ( 3 3 ). 8 ( , ), ), 3 , 3 2
( ), 3 , 3 ( ( , ), 1 1 2 3 4 4 1 2 3 3 1 2 2 1 1 k k k k h y y k f x h y hk hk hk k hk h y
h k f x k h y h k f x k f x y i i i i i i i i i i Bu 4-tartibli
aniqlikka ega usullarda hisoblashlar hajmi 1- va 2-tartiblisiga nisbatan ko‘paygani
bilan hisoblashlarning lokal xatoligi keskin kamayadi. Bu esa hisoblash qadamini
oshirish va o‘z navbatida hisob vaqtini qisqartirish imkonini beradi. 3-misol.
Quyidagi Koshi masalasini Runge-Kutta usuli bilan yeching va natijalarni
taqqoslang. x y, y(0) 1. dx dy Yechish. Ushbu masalaning analitik yechimi:
y(x) 2e x 1 x . Dastlabki qadamlardagi hisoblashlarni qo‘lda bajaramiz: 1-
qadamda: h = 0.1; x0 = 0; y0 = 1 , k1 = 0+1 = 1, 22 k2 = (0+0.25)+(1+(0.25)·(1)) =
1.5, k3 = (0+0.25)+(1+(0.25)·(1.5)) = 1.625, k4 = (0.5)+(1+(0.5)·(1.625)) = 2.3125,
y1 = 1+(0.5/6)[1+2·(1.5)+2·(1.625)+2.3125] ≈ 1.7969. 2-qadamda: y2 ≈ 3.4347 va
hokazo. Qolgan hisoblashlar natijalartini jadvalda va 1.5-rasmda ko‘rish mumkin.
Masalani sonli yechishning MATLAB dasturi: function yp = f(x,y) yp = x + y
function [X,Y] = rk(x,y,x1,n) h = (x1 – x)/n; X = x; x Y = y; y For i = 1:n; k1 =
f(x,y); k2 = f(x+h/2,y+h*k1/2); k3 = f(x+h/2,y+h*k2/2); k4 = f(x+h,y+h*k3); k =
(k1 + 2*k2+2*k3+k4)/6; x = x + h; y = y + h*k; X = [X;x]; Y = [Y;y]; end Hisob
natijalari va ularni taqqoslash jadvali x Eylerning takomillashtirilgan usuli (h=0.1)
Runge-Kutta usuli (h = 0.1) Aniq yechim 0.1 1.1100 1.110342 1.110342 0.2
1.2421 1.242805 1.242806 0.3 1.3985 1.399717 1.399718 0.4 1.5818 1.583648
1.583649 0.5 1.7949 1.797441 1.797443 0.6 2.0409 2.044236 2.044238 0.7 2.3231
2.327503 2.327505 0.8 2.6456 2.651079 2.651082 0.9 3.0124 3.019203 3.019206
1.0 3.4282 3.436559 3.436564 23 1.5-rasm. Runge-Kutta usuli bilan olingan 2-
misolning natijalari grafigi. Bu jadvaldan ko‘rinib turibdiki, Runge-Kutta usuli
ba'zi amaliy masalalarning integral egri chiziqlarini (Koshi masalasining
yechimini) qurishda Eylerning takomillashtirilgan usulidan ham ko‘ra juda ham
samarali natija berar
4. Ingliz matematigi Bruk Teylor matematika faniga o’zining juda ko’p ilmiy
ishlari bilan katta xissa qo’shgan olimlardan biridir. Uning matematika tarixida
buyuk kashfiyotlaridan biri, o’zining 29 yoshida, ya’ni 1715 – yilda yaratgan
nazariyasi
Foydalanilgan adabiyotlar
1.G.P.Ismatullayev M.S.Kasbagenova
Tafakkur bustoni Toshkent-2014](/data/documents/5f0939a8-d131-4958-888c-6e4aa3bc8e8d/page_18.png)

Mavzu: CHekli ayirmali usullar. Adamsning ekstropolyatsiya formulasi Adamsning interpolyatsiya formulasi. Miln ,Runge-Kutta qadamli usuli Reja: Kirish. Asosiy qism. CHekli usullar. 2.Adamsning ekstrapolyatsiya,interpolyatsiya formulasi. 3. Miln,Runge-Kutta qadamli usul. IV.Foydanilgan adabiyotlar.
SO’Z BOSHI Hisoblash mexanikasi tamoyillari bilan boshqariladigan hodisalarni o’rganish uchun hisoblash usullaridan foydalanish bilan bog’liq intizomdir.Paydo bo’lishidan oldin hisoblash fani (ilmiy hisoblashdeb ham yurutiladi) nazariy va ekspremental fanlardan tashqari ‘’uchunchi yo’l,, sifatida hisoblash mexanikasi sub’ekt qabul qilingan amaliy mexanika.Endi u hisoblash fanlari sub-intizomi deb hisoblanadi. Hisoblash mexanikasi fanlararo bog’liq.Uning uchta ustuni mexanika , matematika va kompyuter fanlardir Mexanikaning hisoblash mexanikasi bilan ko’proq bog’liq bo’lgan sohalari suyuqlikning hisoblash dinamikasi,hisoblash termodinamikasi,hisoblash elektromagnitikasi. 1.Differensial va integral tenglamalar klassik analizda qanchalik katta ahamiyatga ega bo`lsa, chekli-ayirmali tenglamalarning roli ham diskret analizda ana shundaydir. Bu paragrafni chekli-ayirmali tenglamalarga baqishlaymiz. Faraz qilaylik,у(х) funksiya biror oraliqda berilgan bo`lsin. Aniqlik uchun bu oraliq 0≤ x<∞ yarim o`qdan iborat bo`lsin. Biror h > 0qadamli x + kh to`rni olib, y(x) ning chekli ayirmalarini tuzamiz: Δy (x),Δ2y(x),...,Δpy(x) Ushbu F(x,y(x),Δy (x),...,Δpy(x))=0 (1.1) ko`rinishdagi tenglama p-tartibli chekli-ayirmali tenglama deyiladi. Bu yerda y(x) izlanayotgan funksiya bo`lib, F(h y0, ...,уp)o`z argumentlari (х, у0, ..., уp) ning o`zgarish sohasida aniqlangan funksiyadir. Agar chekli ayirmalarni funksiyaning qiymatlari orqali ifodalasak (1.1) tenglama quyidagi ko`rinishga ega bo`ladi: Ф (х, у(х), у (x+h), ..., y(x + ph)) = 0. (1.1) Endixningх=nh (п=0, 1,2,...)ko`rinishdagiqiymatlariniolib, y(kh =ykdebbelgilabolsak (1.2) tenglama Q ( n , yn , yn +1, ... yn + p ) = 0 ( n = 0,1,2,...) (1.2) ko ` rinishga ega bo ` ladi . Biz ko ` rinishdagitenglamaningengsoddako`rinishini, ya`niукlarganisbatanchiziqlibo`lgan L(y)=a0(n)yn+p+a1(n)yn+p−1+...+ap(n)yn= f(n) (1.3) tenglamani qaraymiz. Butenglaman - tartiblichiziqli - ayirmalitenglamadeyiladi . Buyerda а i (п) koeffisiyentlarvaf ( n ) ozodhadp ( butunsonlar ) ningixtiyoriyfunksiyalari .
Ozodhadinolgatengb o` lganL ( z )=0 tenglamabirjinslideyiladi . Agar с ilargakonkretqiymatlarberib , Z = z ( n , c 1 ,с2, ..., сп) formuladanqaralayotgantenglamaningbarchayechimlarinitopishmumkinb o` lsa , bundayformulaumumiyyechimdeyiladi . Agarvva у birjinslib o` lmaganL ( v )= htenglamaningxususiyvaumumiyyechimib o` lsa , uholdaz = у- vbirjinslitenglamaningyechimib o` ladi : L ( u - υ ) = L ( u ) - L ( υ ) = h - h = 0. Shundayqilib , birjinslib o` lmagantenglamaningumumiyyechimibirjinslitenglamaningumumiyyech imibilanbirjinslib o` lmagantenglamaningxususiyyechiminingyi g` indisigateng : у= z + υ .Agarbarchasibirdaniganolgatengbo`lmaganс1, с2, ...,стlarmavjudbo`lib, c1u(1)+c2u(2)+...+cmu(m)=0 (1.4) o`rinlibo`lsa, uholdabirjinslitenglamaL(u) =0 ningi(1), i(2),..., i(т) yechimlariargumentningсi. = 0(i = 1,n)dabajarilsa, buyechimlarchiziqlierklideyiladi. Agarz(i)birjinslitenglamaL(z) = 0 ningyechimi ∑i ciz(i) b o` lsa , uholdaularningchiziqlikombinatsiyacihambutenglamaningyechimib o` ladi , chunki L (∑ i ciz(i) ) =∑ i ciL(z(i))=0 (1.5) Qulaylikuchun (1.5) tenglamaningп ¿ 0 qiymatlaruchunqaraymiz. Teorema.Farazqilaylik,barchaп ¿ 0 uchunа0(п) ¿ 0 bo`lib, аi(п)larchegaralanganbo`lsin. UholdaL(z) = 0 birjinslitenglamaningumumiyyechimi z=∑ i=1 p ciz(i) (1.6) bo`lib z(1),...,z(p) funksiyalarL(z) = 0 ningchiziqlierkliyechimlaridir. Isbot. (1.) tenglamani quyidagi (f(n) = 0 bo`lganda) zn+p=− ∑ i=0 p−1ai(n) a0(n)zn+i ko`rinishdayozibolamiz. Agarz0,,z1..., znberilganbo`lsa, (1.4) danketma-ketzp , zp+1 ,…larnitopibolamiz. Demak ixtiyoriy z0,,z1 ,…,zp-1uchun L(z) = 0 tenglama yechimga ega. Bu yechim yagona, chunki qar qanday yechimning qiymati (1.7) tenglamani qanoatlantiradi, bu tenglamadan esa эса zp, zp+1 ,… larning qiymatlari yagona ravishda aniqlanadi. Endi zn(i)orqali L(z) = 0 tenglamaning zj−1 (i)=δij (i,j =1,2, ...,p) shartlarni qanoatlantiruvchi yechimlarini belgilaylik. Bu yechimlar chiziqli erkli sistemani tashkil etadi. Haqiqatan ham
∑ i=1 p cizn (i)=0 (1.8) bo`lsa, u holda j =1,2, ..., p uchun 0=∑ i=1 p cizj−1 (i)=∑ i=1 p ciδij= ci Demak (11.8) tenglik faqat si =0 (i = 1,p ) bo`lgandagina bajariladi va shuning uchun ham z(1),...,z(p) funksiyalar chiziqli erklidir. Endi L(z)=0 ning ixtiyoriy yechimini (1.6) ko`rinishda yozish mumkinligini ko`rsatamiz. Faraz qilaylik, уп L(z) = 0 ning biror yechimi bo`lsin. U holda yn= ∑ i=1 p zi−1zn (i) funksiya bu tenglamaning z0,z1,...,zp−1 dastlabki shartlarini qanoatlantiradigan yechimi bo`ladi. L(z) tenglama yechimining yagonaligidan zn=∑ i=1 p zi−1zn (i) (1.9) kelibchiqadi. Teorema isbot bo`ldi. Endi o`zgarmas koeffisiyentli chiziqli-ayirmali tenglamani L(y)=∑ i=0 p aiyn+1= f()n,ap0 va unga mos keluvchi bir jinsli L(z)= ∑ i=0 p aizn+1=0 (1.10) tenglamani qaraymiz. Oxirgi tenglamaning xususiy yechimini ni ko`rinishda izlaymiz, u holda (∑i=0 p aiλi )λn= 0 Demak,xarakteristik tenglama deb ataluvchi ∑ i=0 p aiλi=0 tenglamaninghar bir yechimiga (1.10) tenglamaning λ i" xususiy yechimi mos keladi. Agar xarakteristik tenglamaning barcha ildizlari tub bo`lsa, u holda p ta har xil yechimga ega bo`lamiz. Xarakteristik tenglamaning har biri k karrali ildiziga (1.10) tenglamaning k ta har xil λn,cn1λn−1,...,cnk−1λn−k+1 (1.11)
yechimlari to`g`ri kelishini ko`rsatamiz. Buni karrali ildizlar haqiqiy bo`lgan hol uchun qarash bilan kifoyalanamiz, chunki aytilgan gaplar kompleks bo`lgan hol uchun ham o`rinlidir. Xarakteristik kop`hadni ko`paytuvchilarga ajratamiz:∑ i=0 p aiλi=ap∏ i=1 p (λ− λ1) Haqiqiy ε>0, ε→ 0 parametrni olib, quyidagi ikki shartni qanoatlantiruvchi λiε ni olamiz: 1) barcha i = 1,2,..., k uchun λiε lar har xil; 2) barcha i ¿ кuchun limx→0λiε= λi Bu ildizlarga moc keladigan xarakteristik tenglamani tuzamiz: 0=ap∏ i=1 p (λ− λiε)=∑ i=0 p aiελi Ko`rinib turibdiki, limx→0aiε=ai Bu xarakteristik tenglamaga ∑ i=0 p aiεzn+1=0 (1.12) ayirmali tenglama mos keladi. Endi faraz qilaylik ε > 0 uchun [1.12] tenglamaning shunday zε,n yechimini ko`rsata olaylikki, ixtiyoriy п> 0uchun limε→0zε,n=zn limit mavjud bo`lsin. Agar limε→0aiε=ai ni hisobga olib, (1.12) tenglamada limitga o`tsak u holda zn limitdagi funksiya (1.10) tenglamaning yechimi ekanligini ko`ramiz. Shunday ketma-ket-liklarni ko`ramizki, ular (1.10) tenglamaning karrali ildiziga mos keladigan xususiy yechimiga yaqinlashsin. Bunday qurishni amalga oshirish uchun bo`lingan ayirmalardan foydalanamiz. Avval ildiz ikki karrali bo`lgan holni ko`ramiz, buning uchun ϕ(λ)= λn deb belgilab, z2ε,n=ϕ(λ1ε,λ2ε)= λ2εn− λ1εn λ2ε− λ2ε birinchi tartibli bo`lingan ayirmani olamiz. Ko`rinib turibdiki, bu funksiya (1.10) tenglamani qanoatlantiradi. Endi limε→0λ1ε= limε→0λ2ε= λ1 ni hisobga olib, limitga o`tamiz: limε→0z2ε,n=limε→0(λ2εn−1+λ2εn−2λ1ε+...+λ1εn−1)=nλ 1n−1 Shunday qilib, biz ikki karrali ildizga mos keladigan yana bir yechimga ega bo`ldik. Endi ning karraligi ikkidan katta bo`lgan holni ko`rib chiqamiz. Buning uchun 5-bobdagi bo`lingan ayirmalar nazariyasiga oid ikkita formuladan foydalanamiz:
